Основные правила дифференцирования

Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x), v=v(x) – две дифференцируемые функции от переменной x.

1. 
2. .
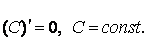
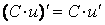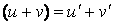3. (справедлива для любого конечного числа слагаемых).
4. .
5. .

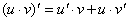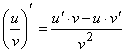а) .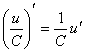

б) .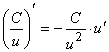

Доказательство формулы 3.

Пусть y = u(x) + v(x). Для значения аргумента x +Δ x имеем y (x +Δ x)= u (x +Δ x) + v (x +Δ x).

Тогда

Δ y = y (x +Δ x) – y(x) = u(x +Δ x) + v(x +Δ x) – u(x) – v(x) = Δ u +Δ v.

Следовательно,

.

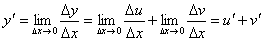Доказательство формулы 4.

Пусть y=u(x)·v(x). Тогда y (x +Δ x)= u (x +Δ x)· v (x +Δ x), поэтому

Δ y = u (x +Δ x)· v (x +Δ x) – u (x)· v (x).

Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u (x +Δ x)→ u(x), v (x +Δ x)→ v(x), при Δ x →0.

Поэтому можем записать

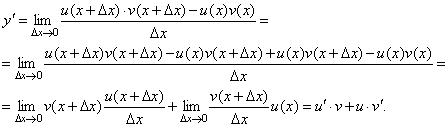
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.

Пусть, например, y=u·v·w. Тогда,

y ' = u '·(v· w) + u ·(v ·w) ' = u '· v ·w + u ·(v '·w + v ·w ') = u '· v ·w + u · v '·w + u·v ·w '.

Доказательство формулы 5.

Пусть 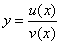. Тогда

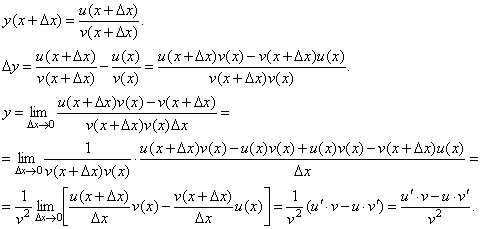
При доказательстве воспользовались тем, что v(x+ Δ x) → v(x) при Δ x →0.