График имеет вертикальные асимптоты, если
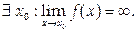
Условие наличия горизонтальной асимптоты – конечный предел
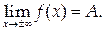
Если этот предел бесконечен, функция может иметь наклонную асимптоту при условии, что
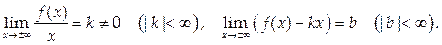
Решение
Исследуем функцию на наличие асимптот разных видов.
1) х = + 1 – точки разрыва 2-го рода, поэтому прямые х = + 1 – горизонтальные асимптоты графика.
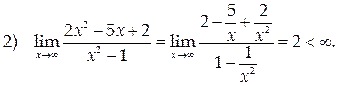
Следовательно, прямая у = 2 – горизонтальная асимптота графика на обоих концах оси Ох. При этом наклонных асимптот у функции быть не может.
Итак, график имеет 3 асимптоты (две вертикальных и одну горизонтальную).
Ответ: 3.
Задача 6.
Асимптоты какого вида имеет график функции
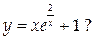
 2015-07-14
2015-07-14 358
358








