Задача 1

Расчетно-графическая работа №1

По дисциплине «Математический анализ»

по теме « Приложение производной к исследованию функций и построению графиков»

Экономика, 1 курс, 1 семестр

Примеры решения задач.

Замечание.

Исследование функции и построение её графика можно проводить по следующему плану:

1. Найти область определения функции. Выделить точки разрыва.

2. Найти асимптоты сначала вертикальные, а затем наклонные.

3. Исследовать функцию на чётность.

4. Определить интервалы возрастания и убывания функции и точки экстремума.

5. Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.

6. Используя результаты исследования построить график функции (при необходимости взять несколько дополнительных точек).

Задача 1.

Исследовать функцию

Решение: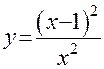

1. Данная функция определена при всех значениях аргумента, исключая х=0.

Область определения функции состоит из двух интервалов:

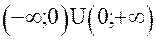. Х=0-точка разрыва функции.

2. Найдем асимптоты графика функции

а) вертикальные.

Найдем односторонние пределы при .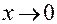

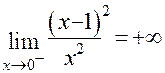
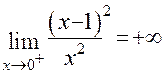
следовательно, х=0-точка бесконечного разрыва и х=0-вертикальная асимптота графика функции.

б) наклонные асимптоты.

Наклонные асимптоты 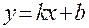найдем, используя формулы

.

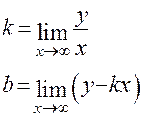Имеем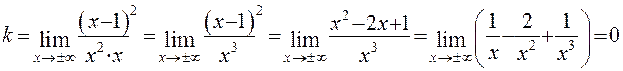

.

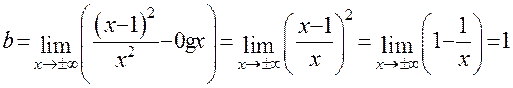Следовательно, прямая у=1 является асимптотой графика функции. (у=1- горизонтальная асимптота, которая является частным случаем наклонной асимптоты при к=0).

3. Функция 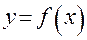является четной, если 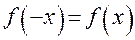и нечетной, если 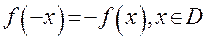. Для нашей функции

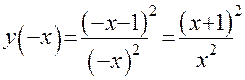. Ни одно из равенств не выполняется, следовательно, функция не является ни четной, ни нечетной.

4. Найдем интервалы возрастания и убывания функции и точки экстремума.

Находим первую производную

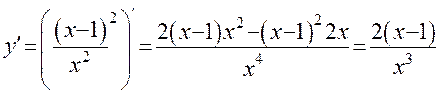
Приравниваем первую производную к нулю и решим уравнение

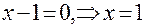-критическая точка.

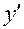не существует при х=0, но в этой точке и сама функция не существует, значит, она не может быть точкой экстремума, но в исследование на возрастание и убывание её включаем. Нанесем на числовую прямую точки х=1 и х=0 и определим знаки производной на каждом промежутке.

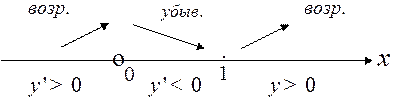
Итак, при x<0; y'>0, значит, функция возрастает. Если 0<x<1; y'<0, функция убывает. Если х>1;y'>0, функция возрастает. При переходе через точку х=1 y' меняет знак с" -"на "+", следовательно, х=1-точка минимум.

У(1)=0. А(1;0)-минимум функции.

5. Найдем интервалы выпуклости и вогнутости графика функции и точки перегиба. Найдем вторую производную

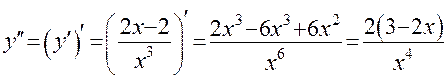
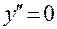при 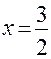. 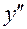не существует при х=0. Т.к функция при х=0 тоже не существует, то она не может являться абсциссой точки перегиба,но в исследование на выпуклость, вогнутость её включаем.

Наносим точки х=0 и x=3/2 на числовую прямую и находим знаки .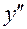

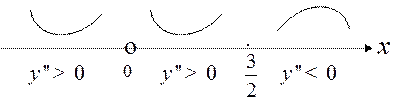При x<0, 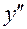>0→график функции вогнутый.

При 0˂x<3/2, 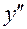>0→график функции вогнутый.

При x>3/2, 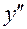<0→график функции выпуклый.

Т.о 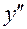меняет знак, следовательно, x=3/2 является абсциссой точки перегиба графика функции.

Найдем ординату у(3/2)=1/9.

Итак, (3/2;1/9)-точка перегиба графика функции.

6. По данным исследования построим график функции

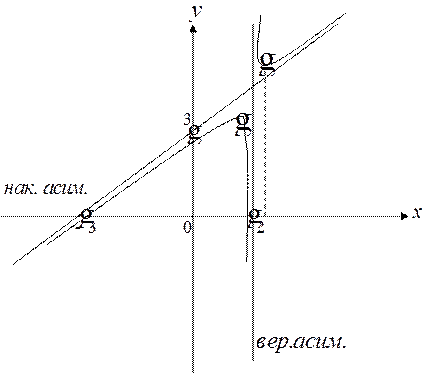Замечание: при построении графика сначала в систему координат внести точки экстремума, точки перегиба и асимптоты.