Определение. Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентаминазывается уравнение вида 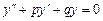 , где
, где 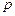 и
и 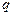 – постоянные величины.
– постоянные величины.
Для практического использования алгоритм решения таких уравнений удобно оформить в виде таблицы:
| Дифференциальное уравнение | 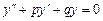
| ||
| Характеристическое уравнение | 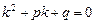
| ||
Дискриминант
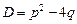
| 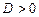
| 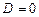
| 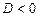
|
| Корни характеристического уравнения | 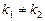
| 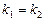
| 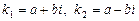
|
| Множества решений | 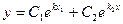
| 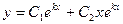
| 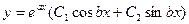
|
Пример 1. Решить уравнение 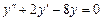 .
.
Решение. Составим характеристическое уравнение 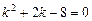 .
.
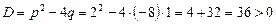 .
.
Следовательно, характеристическое уравнение имеет два различных действительных корня. Определим их: 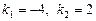 .
.
Общее решение данного уравнения имеет вид 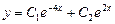 .
.
 2015-07-14
2015-07-14 203
203








