Здесь установлена локальна связь (в точке) величин, описывая электронные поля. Применим теорию Стокса к левым частям уравнений ( ) и (
) и ( ).
).
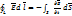 (
(  )
)
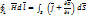 (
(  )
)
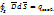 (
(  )
)
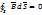 (
(  )
)
Теорема Стокса: циркуляция в  вдоль замкнутого контура
вдоль замкнутого контура  равна потоку вектора
равна потоку вектора 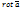 через поверхность
через поверхность  , ограниченную контуром
, ограниченную контуром  ,т.е.
,т.е.
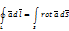
Пусть 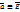
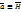
Тогда 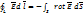
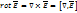
Уравнение (I) примет вид:
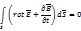
S-любая поверхность, подынтегральное выражение =0, т.е 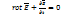
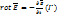
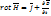
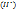
К уравнению III и IV применим математическую формулу теории Остроградского-Гаусса: поток вектора  через замкнутую поверхность S равен
через замкнутую поверхность S равен 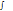 от
от 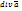 по всему объему
по всему объему  , ограниченному этой поверхностью, т.е.
, ограниченному этой поверхностью, т.е.
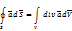
Пусть
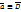
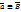
Левая часть уравнения III примет вид:
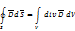
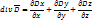
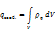
С учетом сказанного, уравнение III в дифференциальной форме:
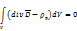
 -произвольный, то
-произвольный, то 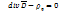
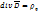
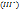
 Аналогично уравнение IV
Аналогично уравнение IV
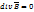
 2015-07-14
2015-07-14 377
377








