Работа силы (сил) над одной точкой

· Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

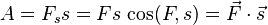
Здесь точкой обозначено скалярное произведение^[4], 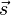— вектор перемещения; подразумевается, что действующая сила 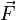постоянна в течение всего того времени, за которое вычисляется работа.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки^[5]:

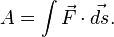
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений 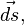если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[6], интеграл определяется^[7] следующим образом:

,

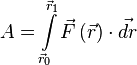где 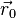и 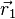— радиус-векторы начального и конечного положения тела соответственно.

· Следствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.