Предел числовой последовательности

Если по некоторому закону каждому натуральному числу п поставлено в соответствие вполне определенное число 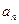, то говорят, что задана числовая последовательность 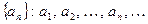. Другими словами, числовая последовательность – это функция натурального аргумента .

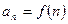Рассмотрим последовательность

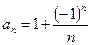
Число А называется пределом числовой последовательности 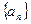, если для любого, даже сколь угодно малого положительного числа 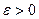, найдется номер N, зависящий от 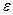, что для всех членов последовательности с номерами n>N верно неравенство .

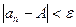Предел числовой последовательности обозначается 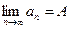. Последовательность, имеющая предел называется сходящейся, в противном случае – расходящейся.

Геометрический смысл предела числовой последовательности заключается в следующем. Число А есть предел числовой последовательности 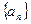, если для любого 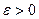найдется номер N, начиная с которого все члены последовательности будут заключены в

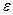-окрестности точки А, какой бы узкой она не была.