ОБЩАЯ ПОСТАВНОКА ЗАДАЧ
Под программированием здесь подразумеваем планирование.
Определение
Задачей линейного программирования будем называть задачу отыскания наибольшего или наименьшего значения линейной функции на некотором множестве.
Задача имеет следующий внешний вид:
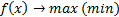
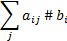
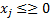
Это система линейного ограничения.
где:
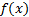 – целевая функция или критерий оптимальности
– целевая функция или критерий оптимальности
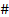 – любой знак
– любой знак
Целевая функция чаще всего имеет вид:
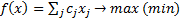
Определение:
Задача линейного программирования называется стандартной, если:
1. 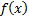 на
на 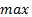
2. 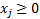 для любых
для любых 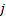
3. Ограничения имеют вид неравенств 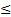 (СЭЛП)
(СЭЛП)
Определение:
Задача линейного программирования называется канонической, если выполняются первой и второе из перечисленных выше условий, а ограничения имеют вид равенств.
Определение:
Множество  называется множеством планов или допустимых решений. Иными словами, если
называется множеством планов или допустимых решений. Иными словами, если 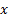 ’ы удовлетворяют решениям задачи, то множество
’ы удовлетворяют решениям задачи, то множество 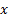 будет планом допустимых решений задачи.
будет планом допустимых решений задачи.
Определение:
План 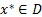 называется оптимальным в задаче на
называется оптимальным в задаче на 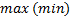 , если
, если 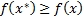
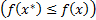 для любых
для любых 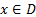 .
.
Рассмотрим несколько задач линейного программирования.
Задача о пищевом рационе.
Имеется три вида продуктов: 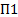 ,
, 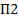 ,
, 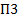 . Из этих продуктов требуется составить пищевой рацион, который должен содержать:
. Из этих продуктов требуется составить пищевой рацион, который должен содержать:
белков не менее 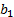 ед.
ед.
углеводов – не менее 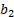 ед.
ед.
жиров – не менее 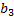 ед.
ед.
Содержание белков, углеводов и жиров в одной единице продукции каждого вида указано в таблице:
| Вид продукции | белки | жиры | углеводы | Стоимость единицы продукции |
 | 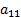 | 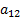 | 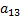 | 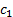 |
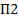 | 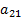 | 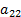 | 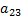 | 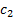 |
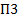 | 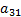 | 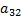 | 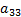 | 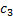 |
Составить пищевой рацион таким образом, чтобы выполнялись условия по белкам, углеводам и жирам, и стоимость рациона была бы минимальной.
Cоставим задачу.
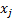 – это количество единиц той или иной продукции.
– это количество единиц той или иной продукции.
Составим ограничения.
Белков в продукции 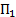 будет
будет 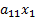 , т. к.
, т. к. 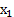 – это количество продукции
– это количество продукции 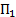 , а
, а 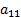 – это количество белков в одной единице продукции. Тогда:
– это количество белков в одной единице продукции. Тогда:
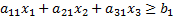
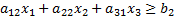
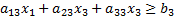
Определим целевую функцию. По условию задачи она стремится к минимуму:
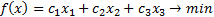
И положим следующее ограничение: количество товаров не может быть отрицательным, т. е. 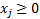 .
.
Таким образом, задача имеет следующий вид:
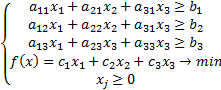
 2015-07-21
2015-07-21 1267
1267