Общий подход к решению задач нелинейного программирования

К задачам нелинейного программирования относятся такие задачи на условный экстремум, в которых не линейны либо целевая функция, либо, по крайней мере, одна из функций, образующих область допустимых решений, либо не линейны и целевая функция и функции-ограничения.

Задача нелинейного программирования (задача НП) в общем виде формулируется следующим образом:

(1.1)

Найти максимум функции

z = f (x₁,x₂,…, x_n)

при условиях

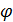₁(x₁,x₂,…, x_n) 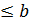₁,

(1.2)

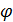₂(x₁,x₂,…, x_n)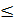 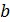₂,

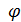_m(x₁,x₂,…, x_n)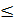 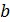_m,

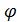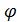где хотя бы одна из функций f, ₁, ₂,.., 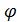_m не линейна.

Предположим, что все эти функции дифференцируемы. Тогда для определения условного экстремума могут быть использованы методы дифференциального исчисления. Процесс решения будет состоять

1) в определении внутри допустимого множества всех стационарных точек функции f, удовлетворяющих условию 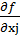=0; j=1,2,…, n;

2) в определении той стационарной точки, которая доставляет наибольшее значение функции f внутри области;

3) в нахождении максимума функции f внутри каждой границы области и выборе наибольшего ее значения по всем границам;

4) в нахождении наибольшего значении функции f в вершинах области;

5) в нахождении глобального максимума функции f.

Как видим, решение задачи НП значительно сложнее решения задачи линейного программирования. Для решения последней требовалось исследовать значение целевой функции лишь в вершинах области, да и то не во всех.