Теорема Куна-Таккера

Введем понятие седловой точки функции многих переменных. Дана некоторая функция Q=Q(x₁,x₂,…, x_n, y₁, y₂,…, y_m) двух групп переменных x₁,x₂,…, x_n и y₁, y₂,…, y_m. Пусть по первой группе переменных функцию Q требуется максимизировать, по второй-минимизировать.

Определение. Точка (x^o₁,x^o₂,…, x^o_n, y^o₁, y^o₂,…, y^o_m) = (X_o,Y_o) называется седловой точкой функции Q, если в ней выполняется следующее неравенство:

Q(X, Y_o) ≤ Q (X_o,Y_o) ≤ Q(X_o,Y).

(4.1)

Рассмотрим следующую задачу выпуклого программирования:

Z = f (x₁,x₂,…, x_n) max,

(4.2)

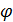₁(x₁,x₂,…, x_n) ≤ 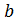₁,

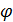₂(x₁,x₂,…, x_n) ≤ 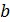₂,

- - - - - - - - - - - - - - -

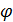_m(x₁,x₂,…, x_n) ≤ 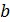_m,

(4.3)

x₁ ≥ 0, x₂ ≥ 0, …, x_n ≥ 0.

Перейдем от этой задачи на условный экстремум к задаче на безусловный экстремум с помощью функции Лагранжа

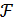(x₁,x₂,…, x_n, λ₁, λ₂,…, λ_m) = f (x₁,x₂,…, x_n) + 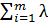_i (b_i – 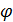_i(x₁,x₂,…, x_n)).

(4.4)

Предположим, что найдена седловая точка функции Лагранжа

(x_o, λ_o) = (x^o ₁, x^o₂,…, x^o_n; λ^o₁, λ^o₂,…, λ^o_m).

Тогда справедливым будет следующее неравенство:

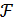(x, λ_o) ≤ 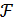(x_o, λ_o) ≤ 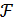(x_o, λ).

Задача отыскания точки (x_o, λ_o) из области определения функции 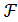(x, λ), удовлетворяющей неравенству (4.4), называется задачей о седловой точке.

Теорема. Точка x_o будет являться решением задачи ВП (4.1)-(4.3) тогда и только тогда, когда существует такая точка λ_o ≥ 0, что точка (x_o, λ_o) является седловой точкой функции Лагранжа 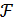(x, λ).