Уравнение состояния

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

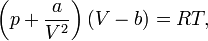
где

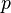— давление,

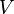— молярный объём,

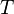— абсолютная температура,

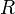— универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка 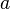учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка 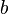— объем молекул газа.

Для 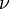молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

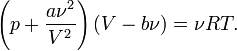
где

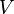— объём,

Правило Вант-Гоффа — эмпирическое правило, позволяющее в первом приближении оценить влияние температуры на скорость химической реакции в небольшом температурном интервале (обычно от 0 °C до 100 °C). Я. Х. Вант-Гофф на основании множества экспериментов сформулировал следующее правило:

Уравнение, которое описывает это правило следующее:

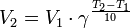
где 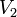— скорость реакции при температуре 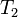, 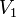— скорость реакции при температуре 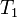, 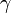— температурный коэффициент реакции (если он равен 2, например, то скорость реакции будет увеличиваться в 2 раза при повышении температуры на 10 градусов).

Следует помнить, что правило Вант-Гоффа применимо только для реакций с энергией активации 60-120 кДж/моль в температурном диапазоне 10-400^oC. Правилу Вант-Гоффа также не подчиняются реакции, в которых принимают участие громоздкие молекулы, например белки в биологических системах. Температурную зависимость скорости реакции более корректно описывает уравнение Аррениуса.

Из уравнения Вант-Гоффа температурный коэффициент вычисляется по формуле:

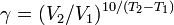
Уравне́ние Арре́ниуса устанавливает зависимость константы скорости химической реакции 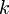от температуры .

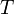Согласно простой модели столкновений химическая реакция между двумя исходными веществами может происходить только в результате столкновения молекул этих веществ. Но не каждое столкновение ведёт к химической реакции. Необходимо преодолеть определённый энергетический барьер, чтобы молекулы начали друг с другом реагировать. То есть молекулы должны обладать некой минимальной энергией (энергия активации 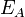), чтобы этот барьер преодолеть. Из распределения Больцмана для кинетической энергии молекул известно, что число молекул, обладающих энергией 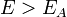, пропорционально 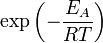. В результате скорость химической реакции представляется уравнением, которое было получено шведским химиком Сванте Аррениусом из термодинамических соображений:

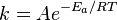
Здесь 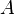характеризует частоту столкновений реагирующих молекул, 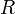— универсальная газовая постоянная.

В рамках теории активных соударений 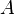зависит от температуры, но эта зависимость достаточно медленная:

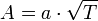
Оценки этого параметра показывают, что изменение температуры в диапазоне от 200 °C до 300 °C приводит к изменению частоты столкновений 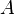на 10 %.

В рамках теории активированного комплекса получаются другие зависимости 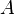от температуры, но во всех случаях более слабые, чем экспонента.

Уравнение Аррениуса стало одним из основных уравнений химической кинетики, а энергия активации — важной количественной характеристикой реакционной способности веществ.

Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением

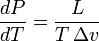
где 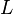— удельная теплота фазового перехода, 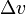— изменение удельного объёма тела при фазовом переходе.

Уравнение названо в честь его авторов, Рудольфа Клаузиуса и Бенуа Клапейрона.