2015-07-21
221
1. Изобразите пример кривых безразличия для выпуклых предпочтений, которые являются локально ненасыщаемыми, но не являются слабо монотонными.
2. Рассмотрите аддитивно сепарабельную дважды дифференцируемую функцию полезности: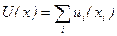 
. Пусть потребитель обладает доходом 
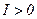, а цены товаров заданы вектором 
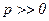. Известно, что 
.
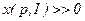а) Покажите, что если для одного товара предельная полезность возрастает в точке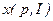 
, то предельная полезность всех остальных товаров в этой точке должна убывать.
б) Докажите, что, если предельная полезность одного товара в точке 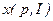возрастает, а предельная всех остальных (в рассматриваемой точке) убывает, то товар с возрастающей предельной полезностью является нормальным, а все остальные товары являются инфериорными.
в) Покажите, что, если все товары имеют убывающую предельную полезность в точке 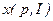, то все товары являются нормальными.
3. Рассмотрите экономику с тремя товарами. Пусть функции маршалловского спроса потребителя на первые два товара имеют вид:
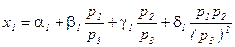и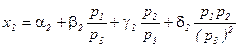 
.
Положите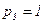 
. Известно, что на приобретение этих трех благ потребитель тратит весь свой доход, равный 
.
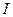а) Найдите спрос на третий товар.
б) Исходя из известных вам свойств функций спроса, найдите ограничения на параметры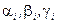 
и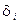 
.
в) Предположим, что параметры удовлетворяют ограничениям, выведенным в пункте (б). Рассмотрите экономическую политику, повлекшую изменение цен с уровня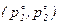 
до уровня 
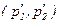. Выведите формулы для оценки изменения благосостояния потребителя.
