1. В уравнение не входит искомая функция, т.е. уравнение имеет вид 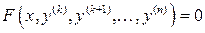 . Порядок уравнения понижается в результате замены
. Порядок уравнения понижается в результате замены 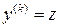 .
.
Пример 1. 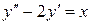 .
.
2. Если в уравнение не входит независимая переменная 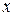 , то уравнение
, то уравнение
имеет вид 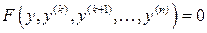 . Для понижения порядка
. Для понижения порядка
уравнения делают замену 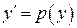 .
.
Пример 2. 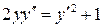 .
.
3. Уравнение является однородным относительно неизвестной функции и
ее производных, т.е. 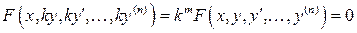 . В этом случае порядок уравнения понижается подстановкой
. В этом случае порядок уравнения понижается подстановкой 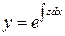 .
.
Пример 3. 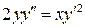 .
.
4. В уравнении присутствует обобщенная однородность в том смысле, что уравнение не изменится, если в нем заменить 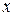 на
на 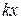 ,
, 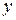 на
на 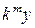 ,
, 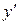 на
на 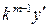 и т.д. В этом случае делается замена
и т.д. В этом случае делается замена 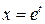 ,
, 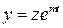 , где
, где 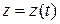 - функция от
- функция от 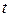 .
.
Пример 4. 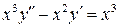 .
.
Проинтегрировать уравнения:
1. 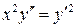 .
.
2. 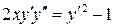 .
.
3. 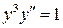 .
.
4. 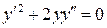 .
.
5. 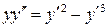 .
.
6. 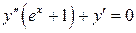 .
.
7. 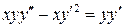 .
.
8. 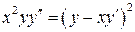 .
.
9. 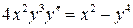 .
.
10. 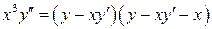 .
.
 2015-07-21
2015-07-21 146
146







