Обратной матрицы

Весьма удобно записывать систему линейных уравнений

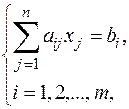(1)

в матричной форме, а именно: если А= (а_ij) – основная матрица системы, а В и X – столбцы свободных членов и неизвестных, то (1) можно записать в виде

A·X=B. (2)

Как и в предыдущем параграфе, предположим, что определитель системы Δ≠0. Отсюда вытекает, что основная матрица системы имеет обратную А^{- 1}. Умножим обе части матричного равенства (2) на матрицу А^{- 1}. Используя ассоциативность умножения матриц и роль единичной матрицы, как единицы при умножении матриц, будем иметь:

A^{- 1} (AX)= A^{- 1} B,

(A^{- 1} A)X= A^{- 1} B,

EX= A^{- 1} B,

X= A^{- 1} B. (3)

Последнее равенство и дает выражение столбца неизвестных через обратную матрицу и столбец свободных членов. Вспомним вид обратной матрицы

A^{- 1} = (А_ji/ Δ) и приравняем j- е элементы столбцов, стоящих в левой и правой частях (3):

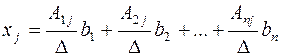
или

.

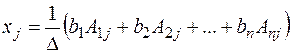Выражение, стоящее в скобках, есть не что иное, как разложение определителя Δ _j (из предыдущего параграфа) по j- му столбцу. Поэтому (3) равносильно

,

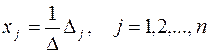и мы снова пришли к формулам Крамера.

Итак, если определитель Δ основной матрицы А системы линейных уравнений отличен от нуля, то существует и притом единственное решение матричного уравнения

АХ=В,

определяемое соотношением

Х=А ^-1 В,

которое эквивалентно формулам Крамера.