Общий случай математической постановки задачи оптимизации

ЗАДАЧИ ОПТИМИЗАЦИИ

На практике часто встречаются такие ситуации, когда достичь какого-то результата можно не одним, а многими различными способами. В подобной ситуации может оказаться и отдельно взятый человек, например, когда он решает вопрос о распределении своих расходов, и целое предприятие или даже отрасль, если необходимо определить, как использовать имеющиеся в их распоряжении ресурсы, чтобы добиться максимального выхода продукции, и, наконец, народное хозяйство в целом. Естественно, при большом количестве решений выбирается наилучшее (оптимальное). Математически это сводится обычно к нахождению наибольшего или наименьшего значения некоторой функции.

Для решения самых разнообразных задач оптимизации необходимо иметь соответствующую математическую модель. В большинстве ситуаций самые различные по содержанию задачи оказываются частными случаями одной задачи оптимизации.

Задача оптимизации в общем случае, включающая три компонента (целевую функцию F, ограничения g_i и граничные условия), имеет следующую математическую постановку:

Найти максимум (или минимум) целевой функции при условии, что переменная х (обычно говорят - точка х) пробегает некоторое данное множество Х.

Символическая запись:

F = f(x₁, x₂, …, x_n) ®max (min) (это функция многих переменных)

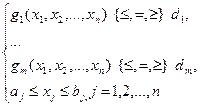(Так задается допустимое множество Х) (1)

где a_j и b_j - нижнее и верхнее предельно допустимые значения x_j.

Задачу (1) можно представить в еще более общей компактной форме записи:

F = f(x_j) ®max (min)

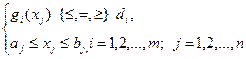(2)

Определенная таким образом задача называется задачей оптимизации.

Граничные условия показывают предельно допустимые значения искомых переменных, и в общем случае они могут быть двусторонними типа a_j£x_j£b_j.

Вместе с тем на практике достаточно нередко возникают следующие частные случаи:

1) в технических, экономических и других видах расчетов искомые величины обычно являются положительными или равными нулю. В этом случае принимается a_j=0, b_j=¥ и накладывается только требование неотрицательности переменных x_j ³ 0;

2) в ряде случаев значение величины x_j может задаваться.

Ограничения обычно выражают определенные зависимости между переменными величинами, которые по своей сути могут быть теоретическими (формульными) и статистическими. Теоретические зависимости обычно справедливы при любых условиях и для их получения не требуется никаких дополнительных измерений. Однако на практике достаточно часто между параметрами модели нет известной функциональной зависимости. Поэтому для получения аналитической зависимости, которая и будет являться ограничением, требуется осуществить сбор и обработку статистических данных.

Так, например, если мы желаем оптимизировать использование общественного транспорта города в течение суток, то нам необходимо знать, как пассажиропоток распределен во времени. Естественно, что такой готовой зависимости нет, и для ее получения потребуется осуществить сбор и обработку статистических данных, чтобы получить определенную аналитическую зависимость, которая и будет тем ограничением, которое следует включить в задачу оптимизации.

Значения переменных, удовлетворяющие заданным граничным условиям и ограничениям, называют допустимымрешением (планом) задачи.

Иногда случается, что в задачу включаются противоречивые по смыслу требования, выполнить которые невозможно. Такая ситуация приводит к несовместным задачам, которые в планировании называют несбалансированными планами (когда нет и не может быть допустимых решений). Обычно же, если задача составлена правильно, то в общем случае она имеет набор допустимых решений.

Чтобы из данного набора допустимых решений лицо, принимающее решение (ЛПР), могло выбрать одно наилучшее (оптимальное), необходимо договориться, как и по какому признаку его найти. ЛПР должно абсолютно точно представлять, в чем заключается оптимальность принимаемого решения, т. е. по какому критерию (от греч. kriterion — мерило, оценка, средство для суждения) принимаемое решение должно быть оптимально.

Критерий часто называют целевой функцией, функцией цели. Критерий в общем случае может оценивать качественные свойства объекта, причем как желательные для субъекта (обычно с максимальным уровнем или значением, например, прибыль, производительность, надежность), так и нежелательные для него (или минимальные — непроизводительные затраты, расход материала, простои оборудования и др.). Если при принятии решения требуется максимизировать какое-то свойство (к примеру, прибыль, производительность или надежность), то в результате решения задачи критерий будет иметь наибольшее значение из всех допустимых решений. Если же требуется минимизировать какое-либо свойство (стоимость, расход материала, время простоев оборудования), то в результате решения критерий будет иметь наименьшее значение из всех допустимых.