Цель: сформировать знания о методах классификации и систематизации первичных данных и способах расчета обобщающих характеристик объекта исследования.
Задачи:
- раскрыть понятия статистической сводки и группировки, показать этапы их выполнения;
- обобщить приемы построения группировок, определить значение разных видов группировок для цели систематизации данных;
- показать основные принципы построения статистических таблиц;
- раскрыть понятие ряда распределения, представить основные показатели распределения и правила построения графиков.
Статистические методы классификации и группировки
Статистическая сводка – это процесс обобщения первичных данных о каждой единице исследуемой совокупности, полученных в ходе статистического наблюдения, с целью выявления типичных черт и закономерностей изучаемого явления/процесса в целом.
Эта задача реализуется путем подсчета итогов по отдельным частям совокупности (группам) и по совокупности в целом, результатом чего является получение системы статистических показателей.
Таким образом, процесс сведения статистических данных разбивается на следующие этапы:
1. Группировка статистических данных;
2. Расчет системы показателей;
3. Табличное и графическое представление результатов.
Комплекс вышеописанных операций иногда называют сложной сводкой. При этом под простой сводкой понимается набор операции по подсчету общих итогов.
Для корректного проведения всех этапов сводки их должен предварять всесторонний теоретический анализ изучаемого явления/процесса.
Массовые явления/процессы, являющиеся предметом изучения статистики, состоят из множества отдельных фактов, каждый из которых обладает как общими признаками, так и широким спектром индивидуальных характеристик. Именно различия свойств отдельных единиц наблюдения обуславливают необходимость их группирования.
Как этап построения статистической сводки, группировка является важнейшим и при этом одним из самых сложных статистических методов, определяющим корректность последующих расчетов и выводов.
Статистическая группировка – это процесс разбиения множества единиц исследуемой совокупности на части по определенным существенным для них признакам с целью получения качественно однородных (в определенном отношении) групп.
Технически процесс группирования статистических данных состоит из следующих этапов:
1. Выбор группировочного признака;
2. Ранжирование совокупности по выбранному группировочному признаку;
3. Определение числа групп;
4. Определение величины интервала;
5. Распределение единиц совокупности по образованным группам.
Группировочный признак, или основание группировки, - это существенный теоретически обоснованный признак, по которому отдельные единицы исследуемой совокупности разбиваются на группы.
Выбор основания группировки определяется целью статистического исследования. Существенность признака означает, что он отражает наиболее характерные черты исследуемого явления в конкретных условиях места и времени. Таким образом, группировочный признак может быть выбран только в результате теоретического анализа.
Основанием группировки могут служить как качественные, так и количественные признаки. Качественные (атрибутивные) признаки отражают состояние единицы наблюдения (например, пол человека, отрасль экономики, форма собственности предприятия и т.д). Количественные признаки имеют числовое выражение (например, курс валют, возраст человека, денежный доход семьи и т.д.).
Количественные признаки, в свою очередь, могут быть дискретными и непрерывными. Дискретные показатели принимают ограниченное число возможных значений, между которыми промежуточных быть не может (например, число детей в семье, число комнат в квартире, число туристических поездок и т.д.). Непрерывные показатели, получаемые обычно в результате измерений и вычислений, могут принимать бесконечное множество значений, т.е. между отдельными значениями непрерывного показателя возможны промежуточные (например, масса продукта, рост человека и т.д.).
При этом важно учитывать, что в процессе статистического наблюдения дискретные признаки часто ведут себя как непрерывные и наоборот. Так, дискретный признак «число жителей» в процессе наблюдения и регистрации на определенный момент тут же меняется, поэтому в справочнике приводится усредненная и округленная информация. Или обратная ситуация, когда непрерывный по сути признак, результат какой-либо операции, фиксируется на определенный момент.
Группировка, в основание которой положен один признак, называется простой. Однако, сложность социально-экономических явлений может потребовать изучения структуры совокупности одновременно по нескольким признакам, взятым в комбинации (например, исследование возрастно-половой структуры населения). Тогда речь идет о сложной группировке.
При построении сложной группировки следует учитывать, что с возрастанием числа группировочных признаков резко увеличивается количество групп. Это, в свою очередь, снижает наглядность итоговой группировки и статистическую устойчивость рассчитываемых показателей.
Сложные группировки могут быть комбинационными и многомерными.
Технически построение комбинационной группировки заключается в последовательном распределении на группы по одному признаку, затем каждой группы на подгруппы по другому признаку и т.д. Как правило, начинают с атрибутивного признака, группы которого качественно различаются между собой. В таблице представлена комбинационная группировка населения по полу и возрасту.
Из таблицы, что при почти одинаковом распределении мужчин и женщин по возрастным группам дошкольного, школьного и трудоспособного возрастов происходит резкое снижение численности мужчин старше трудоспособного возраста по сравнению с женщинами. В основном за счет этой возрастной группы общая численность женского населения превосходит численность мужского.
Таблица
Распределение населения по полу и возрасту в 2008 году
| № п/п | Группы населения по полу | В том числе подгруппы населения по возрасту | Численность, тыс. человек |
| Мужчины | в возрасте 0-6 лет | 5 184,8 | |
| в возрасте 7-15 лет | 6 336,2 | ||
| трудоспособного возраста | 45 928,7 | ||
| старше трудоспособного возраста | 8 267,4 | ||
| ИТОГО по группе | 65 717,1 | ||
| Женщины | в возрасте 0-6 лет | 4 918,5 | |
| в возрасте 7-15 лет | 6 057,9 | ||
| трудоспособного возраста | 43 822,9 | ||
| старше трудоспособного возраста | 21 492,5 | ||
| ИТОГО по группе | 76 291,8 | ||
| ИТОГО по подгруппам | в возрасте 0-6 лет | 10 103,3 | |
| в возрасте 7-15 лет | 12 394,1 | ||
| трудоспособного возраста | 89 751,6 | ||
| старше трудоспособного возраста | 29 759,9 | ||
| ВСЕГО | 142 008,9 |
1) по материалам статистического сборника «Социальное положение и уровень жизни населения России. 2008»
Многомерная группировка строится не последовательно, а одновременно по большому числу признаков с целью формирования качественно однородных групп на основе определенной процедуры оценки близости объектов.
Классификация - это стандартная или нормативная группировка, которая заключается в разбиении отдельных явлений на группы, классы, разряды, секции, виды и т.д. на основании их сходства и различия. Основными отличительными особенностями классификации являются следующие. Во-первых, основанием классификации является качественный признак. Во-вторых, разбиение на классы носит общепринятый стандартный характер и не зависит от целей исследования.
В-третьих, классификации устойчивы, т.е. не изменяются в течение длительного периода времени (изменения происходят лишь с появлением новых классов, разрядов и т.д.). Федеральной службой государственной статистики России (Росстат) ведутся несколько классификаторов (кодированных перечней объектов). Например, макроэкономическая статистика использует классификацию видов экономической деятельности, статистика труда – классификацию профессий и др.
После определения основания группировки проводится ранжирование исследуемой статистической совокупности по группировочному признаку, т.е. все единицы наблюдения располагаются по возрастанию или убыванию значений выбранного признака.
Число групп определяется следующими факторами: задачами исследования, основанием группировки, численностью совокупности, степенью вариации (изменчивости) признака.
В зависимости от цели исследования одна и та же совокупность может быть разбита на разное число групп.
Например, группировка студентов по результатам экзаменационной сессии может быть произведена по двум группам, если задача исследования – выявление успевающих и не успевающих по какому-то предмету; по трем группам, если задача состоит в выявлении неуспевающих, получивших «удовлетворительно» и успевающих на «хорошо» и «отлично» и т.д.
На число выделенных групп влияет и выбранный группировочный признак.
Так, если основанием группировки является качественный признак, то количество групп определяется числом градаций, видов, состояний этого признака. Например, группировка населения по полу (качественный признак) может быть произведена только по двум группам: мужчины и женщины; группировка количества выездов за границу по целям поездки – по пяти группам: служебная, туризм, частная, транзит, обслуживающий персонал и т.д.
Группировка, построенная по количественному признаку, может быть дискретной и интервальной. В дискретной группировке каждая группа представляет собой конкретное значение признака, в интервальной – интервал возможных значений.
Это деление может не соответствовать характеру группируемого количественного признака (дискретный или непрерывный). Дискретный признак может быть сгруппирован интервально, если число его возможных градаций слишком велико для выделения их всех в отдельные группы. Например, при группировке взрослых людей по размеру обуви понадобилось бы минимум 13 групп (размеры с 33 по 45).
В данном случае желательно объединять, например, по два размера в группу, формируя, таким образом, интервальную группировку. Если число возможных значений дискретного признака невелико, то итоговая группировка может быть идеально однородной по данному признаку (например, группировка семей по числу детей). При построении интервальной группировки создаваемые группы будут лишь более-менее однородны.
В таблице представлена дискретная группировка домашних хозяйств по признаку «число детей». Из таблицы видно, что с ростом количества детей в семье происходит перераспределение доли домашних хозяйств с увеличением числа тех, чьи субъективные оценки своих жилищных условий отрицательны. Одновременно с этим, во всех группах по числу детей более половины домохозяйств характеризуют свои жилищные условия лишь как «удовлетворительные».
В таблице представлена интервальная группировка легковых автомобилей по признаку «возраст». Из таблицы видно, что за 2006-7 годы произошло незначительное перераспределение доли машин «среднего возраста» в пользу более «молодых» автомобилей. При этом доля «старых» машин осталась практически без изменений, составляя при этом чуть менее половины всего парка.
Таблица
Распределение домашних хозяйств, имеющих детей в возрасте до 16 лет, по степени удовлетворенности своими жилищными условиями в 2007 г. (в процентах от общего числа домашних хозяйств соответствующей категории)
| Группы домашних хозяйств по числу детей | Домохозяйства, оценивающие свои жилищные условия как: | ||||
| отличные | хорошие | удовлет-ворительные | плохие | очень плохие | |
| 2,4 | 32,3 | 53,0 | 10,6 | 1,4 | |
| 2,5 | 31,0 | 53,3 | 10,7 | 2,2 | |
| 3 и более | 1,2 | 21,8 | 53,7 | 17,8 | 5,5 |
1) по материалам статистического сборника «Социальное положение и уровень жизни населения России. 2008»
Таблица
Возрастная структура парка легковых автомобилей в 2006 -2007г. (на конец года, в процентах к итогу) 1
| Группы легковых автомобилей по числу лет эксплуатации | ||
| до 5 | 23,3 | 25,0 |
| 5-10 | 27,8 | 26,7 |
| более 10 | 48,9 | 48,3 |
| ВСЕГО |
1) по материалам статистического сборника «Социальное положение и уровень жизни населения России. 2008»
Определение числа групп для количественного признака зависит от степени однородности статистической совокупности.
Если исходная совокупность качественно разнородна, то при построении группировки по количественному признаку границы групп определяются там, где количество переходит в новое качество.
Если исследуемая совокупность качественно однородна, то решающее значение для определения количества групп имеют численность совокупности и уровень колеблемости группировочного признака. Итоговым критерием при этом является получение максимально однородных при этом достаточно наполненных групп.
Каждая образованная группа должна быть «обеспечена» достаточным количеством наблюдений, так как погашение случайного и выявление общего, существенного для исследуемого явления/процесса происходит лишь при расчетах по достаточно большим группам. Показатели же, исчисленные по малочисленным группам, не будут корректными и устойчивыми.
При прочих равных условиях, чем больше степень изменчивости признака, тем больше следует образовывать групп, так как это будет способствовать более точному описанию характера изучаемого объекта/процесса. Однако, слишком большое число групп затрудняет выявление закономерностей и автоматически приводит к тому, что в каждую группу попадет меньшее число наблюдений, что снизит статистическую устойчивость рассчитанных впоследствии показателей.
Приемы построения группировок.
Для определения количества групп могут быть использованы стандартные статистические процедуры. Наиболее распространенная из них основана на использовании формулы американского ученого Стерджесса:
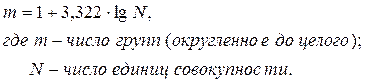
Ограничением формулы Стерджесса является необходимость большого числа наблюдений и близости распределения группировочного признака к нормальному.
После определения числа групп формируются интервалы группировки – значения признака, лежащие в определенных границах.
Величина интервала – это разница между верхней и нижней границами интервала, т.е. максимальным и минимальным значениями соответственно.
Обозначение границ интервалов зависит от характера группируемого признака. Если в основание группировки положен непрерывный признак, то верхняя граница i -го интервала совпадает с нижней границей i+1 -го. Если же группируется дискретный признак, то нижняя граница i+1 -го интервала равна верхней границе i -го плюс 1. В таблице представлены границы групп при распределении людей по возрасту. В варианте I возраст понимается как непрерывная величина, а в варианте II – как дискретная. В этом примере в обоих случаях ширина интервалов одинакова и равна 10 годам.
Таблица
Варианты построения групп для признака «возраст»
| № группы | Вариант I | № группы | Вариант II |
| Возраст, лет | Возраст, лет | ||
| До 30 | 20 – 29 | ||
| 30 – 40 | 30 – 39 | ||
| 40 – 50 | 40 – 49 | ||
| 50 и выше | 50 и выше | ||
| Границы групп, если возраст измеряется с точностью больше года. | Границы групп, если под возрастом понимается число исполнившихся лет. |
По наличию границ различают открытые и закрытые интервалы. Открытыми называются интервалы, для которых определена только одна граница: верхняя (если интервал первый) или нижняя (если интервал последний). В закрытых интервалах определены обе границы.
Для последующих расчетов величина открытого интервала принимается равной величине интервала, смежного с ним. Так, в варианте I таблицы величина первого интервала принимается равной величине второго, а последнего – величине предпоследнего, т.е. десяти годам.
Если по данному правилу получается, что открытый интервал начинает включать в себя теоретически невозможные значения, то его ширина должна определяться логикой явления/процесса. Например, в таблице величина второго интервала равна четырем минутам. В этом случае величина открытого интервала не может быть равна также четырем минутам, так как это означало бы, что нижняя граница первого интервала была бы отрицательна, что применительно к временной характеристике невозможно. Значит, в качестве первого интервала логично принять диапазон от нуля до трех минут.
Таблица
Группировка операторов диспетчерской по среднему времени обработки заказа (цифры условные)
| № группы | Среднее время обработки заказа, мин | Количество операторов, чел |
| До 3 | ||
| 3 – 7 | ||
| 7 и выше | ||
| ВСЕГО |
При формировании границ по представленному в варианте I таблицы типу необходимо определиться, к каким группам относятся единицы наблюдения, значения признака у которых совпадают с граничными. Для этого определяют, какая из границ, нижняя или верхняя, будет формироваться по принципу «включительно», а какая – по принципу «исключительно». Выбранный подход должен быть реализован одинаково для всех интервалов. Для определенности могут также использоваться открытые интервалы. В нашем примере нижняя граница формируется по принципу «включительно», а верхняя, соответственно, - «исключительно».
По величине интервала различают равноинтервальные (величина интервала одинакова для всех групп) и неравноинтервальные (величина интервала разнится от группы к группе) группировки. Неравноинтервальные группировки, в свою очередь, подразделяют на прогрессивно возрастающие/убывающие, равнонаполненные, специализированные и произвольные.
Если изучаемый признак варьирует в сравнительно узких границах и его распределение более или менее равномерно, то целесообразно строить группировку с равными интервалами. Величина интервала при этом определяется по формуле:
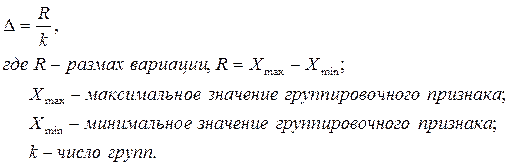
При определении размаха вариации важно, чтобы максимальное и/или минимальное значения не были в определенном смысле «аномальными», т.е. сильно отличающимися от смежных с ними значений признака. В противном случае следует определять разницу значений, которые несколько больше минимального и меньше максимального.
Если полученное значение величины интервала требует округления, то оно должно производиться в большую, а не в меньшую сторону, иначе часть наблюдений может не попасть и итоговую группировку.
Далее определяются границы каждого интервала по следующей схеме:
| № интервала | Границы интервала |
 | |
 | |
| … | |
| k | 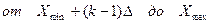 |
Например, пусть статистическая совокупность состоит из 40 туристических компаний, показатели выручки которых варьируют от 50 млн.долл до 650 млн.долл, что является, соответственно, минимальным и максимальным значениями признака. Тогда по формуле Стерджесса получаем: 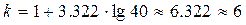 . Величина интервала для построения равноинтервальной группировки определяется следующим образом:
. Величина интервала для построения равноинтервальной группировки определяется следующим образом: 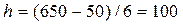 (млн.долл.). Таким образом, совокупность компаний будет разделена по показателю выручки на шесть равных групп: [50-150], [150-250], [250-350], [350-450], [450-550], [550-650] (млн.долл.).
(млн.долл.). Таким образом, совокупность компаний будет разделена по показателю выручки на шесть равных групп: [50-150], [150-250], [250-350], [350-450], [450-550], [550-650] (млн.долл.).
Хотя группировки с равными интервалами предпочтительнее ввиду простоты их последующей обработки, характер изменения большинства социально-экономических явлений не отвечает требованиям, предъявляемым к равноинтервальной группировке. Если исследуемый признак варьирует значительно и неравномерно, возникает необходимость строить неравноинтервальную группировку.
Один из возможных подходов к формированию границ групп основан на использовании арифметической или геометрической прогрессии. В этом случае величина интервалов определяется формулами соответственно.
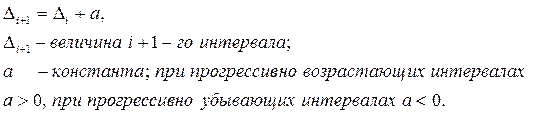
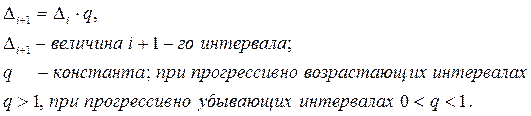
Данный подход к определению величины интервалов может быть использован, например, при группировке городов по числу жителей. Невозможность построения равноинтервальной группировки в данном случае связана с большим количеством малонаселенных городов и незначительным числом «городов-миллионников».
Как правило, при исследовании выручки по результатам деятельности компании любой отрасли «прогрессивный» подход оказывается более целесообразным, чем формирование равных интервалов. Это продиктовано тем, что число малых предприятий с небольшой выручкой значительно превышает число крупных предприятий с высокими показателями.
Описанные выше технические способы определения величины интервалов не гарантируют, что не появятся группы малочисленные или вообще «пустые», в которые не попало ни одно наблюдение. Если это произошло, необходимо изменить число групп и/или величины интервалов, так как подобная группировка является некорректной.
Для обеспечения статистической устойчивости показателей, исчисляемых для отдельных групп, может использоваться равнонаполненная группировка, в которой число наблюдений в каждой группе примерно одинаковое и определяется по формуле:
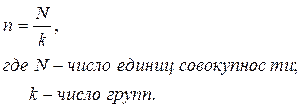
Если полученное n не целое и/или в совокупности есть повторяющиеся значения признака, то число наблюдений в каждой группе может различаться. При этом надо стремиться к тому, чтобы эти различия были незначительны.
Если для реализации задач исследования необходимо устанавливать границы групп там, где количество переходит в новое качество, пользуются специализированными интервалами. Так, в группировке населения по возрасту для оценки трудовых ресурсов границы групп возрастов могут устанавливаться согласно категориям: моложе трудоспособного возраста (до 16 лет), трудоспособный возраст (для женщин с 16 до 54 лет, для мужчин с 16 до 59 лет) и старше трудоспособного возраста (для женщин старше 54 лет, для мужчин старше 59 лет).
Границы групп могут определяться и произвольно, когда ни один из вышеописанных методов не дал хороших результатов.
Заключительным этапом построения группировки является разделение единиц исследуемой статистической совокупности на группы по выбранному (одному или нескольким) группировочному признаку.
Задачи группировки. Типологические, структурные, аналитические и комбинационные группировки.
Метод группировок позволяет решить следующие задачи:
1. Выделение социально-экономических типов явлений;
2. Изучение структуры явления и структурных сдвигов в нем;
3. Выявление связи и зависимости между явлениями.
В зависимости от решаемых задач различают следующие виды группировок: типологическая, структурная, аналитическая группировки.
Типологическая группировка – это процесс разбиения изучаемой качественно разнородной совокупности на однородные группы, характеризующие социально-экономические типы явления.
Являясь, по сути, классификацией, типологические группировки обычно строятся на первом этапе обобщения первичной статистической информации, которая чаще всего неоднородна. При этом важно понимать, что в зависимости от цели исследования одна и та же совокупность может быть качественно однородной и неоднородной. Например, совокупность промышленных предприятий однородна для целей оценки каких-либо производственных характеристик и неоднородна для оценки налогообложения, так как в последнее зависит от формы собственности, от наличия льгот и т.д.
Примерами типологических группировок являются группировки населения по общественным группам, предприятий по форме собственности, видам экономической деятельности и др.
Изучение существующих типов социально-экономического явления в динамике позволяет выявить изменения в соотношениях между ними, появление новых типов или отмирание старых.
При построении типологической группировки идентификация типов исследуемого социально-экономического явления должна основываться на его всестороннем теоретическом анализе, что зачастую представляет большую сложность из-за нечетких различий между типами.
Типологическая группировка может иметь в основе как качественный, так и количественный признак. При этом установление границ интервалов не может быть произвольным, а определяется точками перехода от одного типа к другому, т.е. являются специализированными.
Типологическая группировка представлена в таблице. В данном примере в признаке «форма собственности» выделено пять групп (видов). Анализ показателя среднегодовой численности занятых в динамике позволяет проследить зарождение нового вида явления. Видно, что в 1980 году многих форм собственности не существовало, а, начиная с 1990 года, происходит значительное снижение числа занятых в государственных и муниципальных образованиях при одновременном росте занятых в частной сфере и компаниях, находящихся в иностранной и совместной собственности. Так как при этом общее число занятых снизилось не сильно, можно сделать вывод, что такие изменения произошли вследствие «перехода» занятых из одной сферы в другую.
Таблица
Среднегодовая численность занятых в экономике по формам собственности (тысяч человек)
| … | |||||
| ВСЕГО в экономике в том числе по формам собственности: | |||||
| государственная, муниципальная | |||||
| Частная | |||||
| собственность общественных и религиозных организаций (объединений) | … | ||||
| смешанная российская | … | ||||
| иностранная, совместная российская и иностранная | … |
Структурная группировка – это процесс разбиения качественно однородной совокупности на группы, характеризующие структуру изучаемого явления по какому-либо варьирующему признаку.
Примерами структурных группировок являются группировки населения по возрасту, месту проживания; предприятий по численности занятых, стоимости основных фондов и др.
Изучение структуры социально-экономического явления предполагает анализ не только его составных частей, но и соотношений между ними и изменений в этих соотношениях с течением времени.
Основное требование к формируемым группам при образовании структурной группировки заключается в недопущении выделения «пустых» и малочисленных интервалов. При этом допускается, что первая и последняя группы могут содержать незначительное число наблюдений. Если же такие «провалы» встречаются в срединных интервалах, чаще всего это говорит о том, что произошло смешение разных типов явления и исходная совокупность качественно неоднородна.
Структурная группировка позволяет делать выводы о том, какие значения в исследуемой совокупности встречаются чаще всего, какие – реже всего; каков характер изменения структуры совокупности в целом (равномерный или неравномерный).
Структурная группировка представлена в таблице. Данные группировки показывают, что в 2005 году более 49% населения имело среднедушевой доход ниже 6000 руб. в месяц, а оставшиеся чуть более 50% практически равномерно распределялись по четырем доходным группам от 6000 до 20000 руб. в месяц.
Следующие три года демонстрируют некоторое перераспределение долей населения из малообеспеченных групп в пользу «среднего класса» и появление групп более высоких доходов. Однако, окончательный вывод по этим данным сделать нельзя, так как величина среднедушевого денежного дохода здесь представлена в номинальном выражении, т.е. не скорректирована на индекс потребительских цен. Таким образом, для анализа необходимо сопоставить эти данные с реальными доходами населения.
Таблица
Распределение населения по величине среднедушевого денежного дохода (в процентах) 1
| Все население в том числе со среднедушевыми денежными доходами, руб. в месяц: | ||||
| до 4000,0 | 28,9 | 20,5 | 14,3 | 9,8 |
| 4000,1–6000,0 | 20,3 | 17,7 | 14,8 | 12,0 |
| 6000,1–8000,0 | 14,9 | 14,7 | 13,6 | 12,1 |
| 8000,1–10000,0 | 10,3 | 11,2 | 11,3 | 10,9 |
| 10000,1–15000,0 | 13,9 | 17,1 | 19,1 | 20,1 |
| 15000,1–20000,0 | 11,7 | 8,4 | 10,6 | 12,4 |
| 20000,1–30000,0 | ... | 10,4 | 9,6 | 12,4 |
| свыше 30000,0 | ... | ... | 6,7 | 10,3 |
Аналитическая группировка – это группировка, позволяющая выявить наличие взаимосвязи между различными признаками изучаемого явления и направление этой связи.
Процесс построения аналитической группировки предполагает разделение всех признаков изучаемой совокупности на две группы: факторные, которые влияют на остальные признаки, и результативные, которые изменяются под этим влиянием.
В отличие от других статистических методов анализа взаимосвязи к аналитическим группировкам предъявляется только одно требование – качественная однородность совокупности.
В зависимости от глубины исследования взаимосвязей могут быть построены собственно аналитическая группировка, комбинационная группировка и многомерная группировка.
Построение собственно аналитической группировки заключается в разбиении качественно однородной совокупности на группы по факторному признаку и подсчетом соответственно этим группам среднего значения одного или нескольких результативных признаков с целью выявления между ними взаимосвязи и определения ее направления. При группировании факторного признака стараются сформировать равные или равнонаполненные интервалы.
Систематический рост или снижение среднего значения результативного признака в результате возрастания значений факторного подтверждает наличие между ними прямой или обратной связи соответственно. Бессистемное изменение среднего значения результирующего признака свидетельствует об отсутствии связи с данным фактором.
Комбинационная группировка позволяет более детально оценить зависимость между признаками и направление этой связи. Построение комбинационной группировки для описания связи двух признаков заключается в последовательном разделении групп факторного признака на подгруппы результативного. Желательно, чтобы интервалы формируемых групп были равными или равнонаполненными.
Для оценки наличия и направления связи анализируются максимальные по столбцам или по строкам частоты. Если они располагаются вдоль диагонали, идущей от левого верхнего угла к правому нижнему, то связь между признаками прямая и близкая к линейной. Если максимальные частоты находятся на противоположной диагонали (от правого верхнего угла к левому нижнему), то связь обратная и близкая к линейной. Если же расположение максимальных частот хаотично, связи между признаками нет.
Многомерные группировки позволяют оценить разнонаправленные взаимосвязи большого числа признаков.
Группировки, построенные для разных субъектов за один период времени или для одного субъекта в динамике, позволяют провести анализ изменения характеристик исследуемого явления в различных условиях места и времени соответственно. При этом для целей сравнения группировки должны быть приведены к сопоставимому виду. Эта задача решается с помощью метода вторичной группировки. При этом данный метод снимает проблему сопоставимости лишь в части различий в числе групп и величине интервалов и не касается вопроса сопоставимости исходных данных и процедуры наблюдения.
В отличие от первичной группировки, формирующейся на основе первичных данных, материалом для вторичной служит ранее осуществленная группировка.
Таким образом, вторичная группировка – это процесс перегруппирования уже имеющейся группировки, т.е. создание на ее основе новых групп.
Технически вторичная группировка может быть осуществлена одним из двух способов: объединением первоначальных интервалов или долевой перегруппировкой.
Объединение первоначальных интервалов используется при переходе от более мелких к крупным интервалам, если при этом новые границы совпадают со старыми.
Долевая перегруппировка используется, если для отнесения к той или иной группе в новых границах необходимо определить, какая часть единиц совокупности перейдет из старых групп в новые. Технически долевая перегруппировка заключается в закреплении за каждой группой определенной доли единиц совокупности и распределении этой доли по новым границам при допущении о том, что распределение единиц совокупности внутри каждой группы равномерное.
Статистические таблицы. Их виды и принципы построения.
На втором этапе сведения данных переходят к подсчету итогов по группам и совокупности в целом. Предварительно результаты построения группировок оформляются табличным способом.
Статистическая таблица – это таблица, содержащая сводные числовые характеристики изучаемой совокупности по одному или нескольким логически взаимосвязанным признакам.
Основа (остов) статистической таблицы представлена на рис.
Название таблицы* (общий заголовок)
| Наименование подлежащего | Наименование сказуемого | ||||||
| Верхние заголовки | |||||||
| А | Б | В | … | ||||
| Боковые заголовки | |||||||
| Итоговая строка | Итоговая графа | ||||||
*Примечания к таблице
Подлежащее статистической таблицы – это характеризующийся цифрами объект изучения. Им могут быть единицы совокупности, группы единиц или совокупность в целом. Например, фирмы, регионы, временные периоды и др. Обычно подлежащее таблицы располагается слева, в наименовании строк.
Сказуемое статистической таблицы – это система показателей, являющаяся результатом сводки и характеризующая объект изучения. Обычно сказуемое представлено верхними заголовками, т.е. наименованиями граф, которые располагаются слева направо в логической последовательности.
Общий заголовок – это основное содержание таблицы, представленное в сжатой и ясной форме, с указанием места и времени, к которым относятся составляющие ее сведения.
В зависимости от характера подлежащего, различают простые, групповые и комбинационные статистические таблицы.
Подлежащее простой таблицы представляет собой простой перечень объектов, территорий, хронологических дат, т.е. не предусматривает группировки единиц наблюдения. Подлежащее групповой таблицы содержит группировку единиц совокупности по одному количественному или качественному признаку. Подлежащее комбинационной таблицы содержит последовательную группировку единиц совокупности одновременно по нескольким признакам, т.е. комбинационную группировку.
В зависимости от глубины разработки сказуемого, различают простые и сложные статистические таблицы. При простой разработке сказуемого формирующий его показатель не подразделяется на подгруппы. Сложная разработка сказуемого, напротив, предполагает такое деление, что позволяет охарактеризовать каждую группу или единицу объекта разной комбинацией признаков.
При оформлении статистической таблицы необходимо придерживаться следующих правил:
1. Компактность и наглядность таблицы; отсутствие избыточных, второстепенных данных; представленные данные должны непосредственно отражать изучаемое явление;
2. Краткость формулировок всех заголовков таблицы;
3. Указание единиц измерения всех показателей: в заголовке, если они одинаковы, и в наименованиях строк и граф, если разные; использование общепринятых сокращений: чел., руб. и т.д.;
4. Формирование объединяющих заголовков при наличии в наименованиях подлежащего или сказуемого общих терминов;
5. Расположение взаимосвязанных данные в соседних графах;
6. Логичность в последовательности расположения элементов подлежащего и сказуемого (от частного к общему, от абсолютных величин к средним и относительным и т.д);
7. Одинаковая степень точности в округлении числовых данных;
8. Правильное отображение отсутствия данных: прочерк - при отсутствии явления, «нет сведений» или «…» - при отсутствии информации о явлении; в не подлежащих заполнению ячейках ставится «Х»; если значение составляет величину меньше принятой точности, ставится (0,0) или (0,00) и т.д.
9. Необходимость итоговых строк/граф в групповых и комбинационных таблицах; если они завершают таблицу, используют слова «Итого» или «Всего», если открывают – дополняются словами «в том числе» с последующей конкретизацией.
После чтения таблицы, т.е. ознакомления с содержанием, производится ее анализ, который состоит в выявлении особенностей исследуемого явления и основных тенденций его развития. Процедура анализа при этом проходит обычно от общих итогов к частным с выявлением наиболее характерных черт, сопоставлением частей и формулированием общих выводов из таблицы.
Ряды распределения: дискретные, интервальные. Построение интервальных рядов. Частоты, частости, плотности распределения. Кумулятивные ряды.
Составной частью операций по обработке полученных при группировании данных является построение ряда распределения.
Ряд распределения – это упорядоченное распределение единиц совокупности по группам по какому-либо варьирующему признаку.
Ряд распределения строится, исходя из принципов статистической группировки. Технически это реализуется с помощью простой группировки интересующего признака, в которой каждому значению или интервалу поставлено в соответствие количество единиц совокупности, удовлетворяющих этому значению/интервалу.
Таким образом, ряд распределения состоит из двух структурных элементов: вариант и частот и/или частостей.
Варианта, 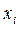 – это конкретное значение варьирующего признака в ряду.
– это конкретное значение варьирующего признака в ряду.
Частота, 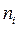 – численность отдельных вариант или каждой группы вариант, показывающая, как часто встречаются эти значения в ряду распределения. Сумма частот по всем группам равна объему совокупности, т.е.:
– численность отдельных вариант или каждой группы вариант, показывающая, как часто встречаются эти значения в ряду распределения. Сумма частот по всем группам равна объему совокупности, т.е.:
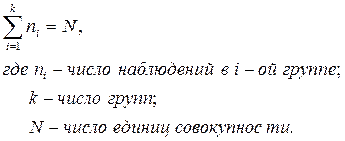
Частость, 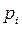 – это частота, выраженная в долях единицы или в процентах к итогу. Сумма частостей по всем группам равна 1 или 100% соответственно, т.е.:
– это частота, выраженная в долях единицы или в процентах к итогу. Сумма частостей по всем группам равна 1 или 100% соответственно, т.е.:
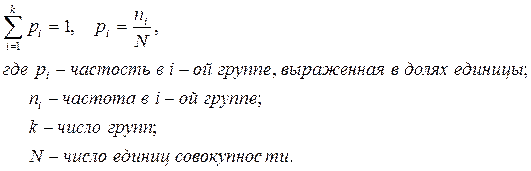
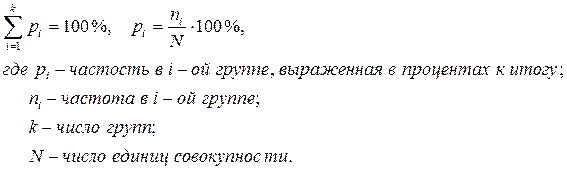 В зависимости от признака, лежащего в основании, различают атрибутивные и вариационные ряды распределения. Так как ряд распределения является, по сути, группировкой, то виды рядов распределения полностью соответствуют описанным выше возможным градациям группировок.
В зависимости от признака, лежащего в основании, различают атрибутивные и вариационные ряды распределения. Так как ряд распределения является, по сути, группировкой, то виды рядов распределения полностью соответствуют описанным выше возможным градациям группировок.
Атрибутивный ряд распределения – это ряд, построенный по качественному признаку.
Вариационный ряд распределения – это ряд, построенный по количественному признаку. Характер вариации последнего может быть дискретным или непрерывным. Соответственно, различают дискретные и интервальные вариационные ряды. Как и при группировании, если число возможных градаций дискретного признака велико, для него строится интервальный вариационный ряд.
Например, если выбрать один интересующий год, то таблица легко трансформируется в атрибутивный ряд распределения занятых по формам собственности в выбранном году, а таблица - в интервальный ряд распределения населения по среднедушевому доходу.
Изучение рядов распределения позволяет выявить наличие и определить характер закономерности в изменении частот с изменением значений варьирующего признака, т.е. проследить закономерности распределения. Закономерности распределения призваны отразить основные свойства изучаемого явления.
При этом актуальным становится требование однородности, предъявляемое к структурным группировкам, в противном случае произойдет смешение распределений, отражающих разные явления. Косвенным подтверждением этого может служить описанный выше вариант появления при группировании малочисленных срединных интервалов.
Выявление подлинной закономерности может затруднить и неверная интерпретация результатов построения интервального вариационного ряда, который может быть равноинтервальным и неравноинтервальным.
При построении неравноинтервального вариационного ряда распределения сравнение частот по группам неправомерно, так как изменение границ интервалов может привести к совершенно противоположным выводам. Следовательно, для корректного отражения распределения признака необходимо избавиться от влияния величины интервала, что осуществляется путем перехода от частот/частостей к плотности распределения.
Абсолютная плотность распределения, 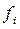 - это частота, рассчитанная на единицу интервала, т.е.:
- это частота, рассчитанная на единицу интервала, т.е.:
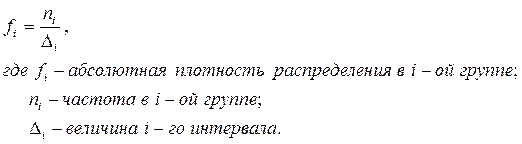
Относительная плотность распределения, 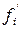 - это частость, рассчитанная на единицу интервала, т.е.:
- это частость, рассчитанная на единицу интервала, т.е.:
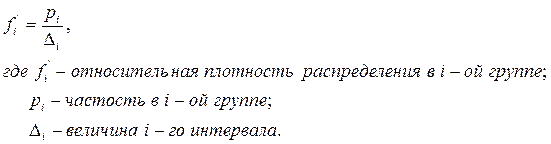
Для возможности сопоставления распределений дискретных и интервальных величин используется универсальный подход, основанный на расчете накопленных частот/частостей. Эти величины определяются путем последовательного суммирования частот/частостей по группам с подсчетом итогов к концу каждой группы.
Накопленная частота/частость, 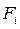 /
/ 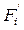 - это число/доля единиц совокупности со значением признака не больше заданного, т.е.:
- это число/доля единиц совокупности со значением признака не больше заданного, т.е.:
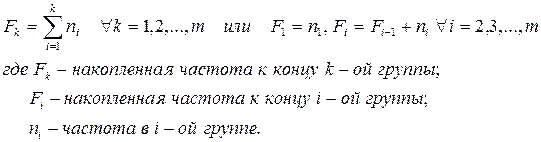
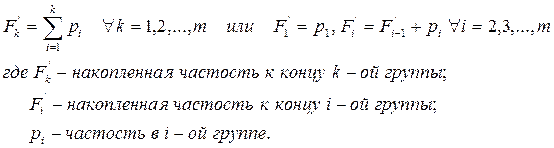
Эти величины, будучи рассчитаны через частоты/частости, не могут быть отрицательны (значение «ноль» они принимают к началу первого интервала), а их максимум ограничен объемом совокупности. К концу последней группы этот максимум должен быть достигнут. Кумулятивный характер накопленных частот/частостей подразумевает, что с возрастанием групповых значений их величины могут только увеличиваться. Таким образом,:
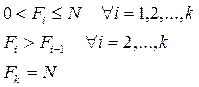
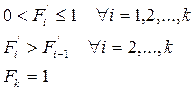
Если в какой-то группе значение накопленной частоты/частости совпадает ее предыдущим значением, значит, рассматриваемая группа не содержит ни одного наблюдения, т.е. является «пустой», что свидетельствует о необходимости перегруппировки.
Обратная процедура – расчет частот/частостей через накопленные частоты/частости – также возможна:
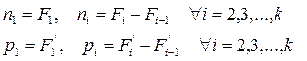
Графическое представление статистических данных.
Удобнее всего анализировать ряды распределения с помощью их графического представления. Наряду с таблицами, график – это метод обобщения исходной информации. Графики позволяют более наглядно и доступно для восприятия отразить интересующие характеристики, взаимосвязи, тенденции в исследуемом явлении.
Статистический график – это чертеж, отображающий характеристики той или иной статистической совокупности с помощью геометрических образов или знаков. В статистике используется большое множество графических изображений различающихся и по выбранной основе графика (линейные, плоскостные, объемные), и по способу построения (диаграммы, статистические карты).
Для правильного построения графика необходимо выполнение набора правил: от внешнего оформления (название графика, подписи масштабных шкал, пояснения) до формирования основных элементов графика (графический образ, поле графика, пространственные и масштабные ориентиры).
Применительно к рядам распределения используют следующие графические изображения: полигон, гистограмма, кумулята, огива. Все эти графики строятся в прямоугольной системе координат.
Полигон – графическое изображение дискретного вариационного ряда распределения, дающее представление о характере изменения его частот. Для построения полигона по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, по оси ординат – частоты или частости.
Полигон представляет собой точки пересечения абсцисс и ординат, которые иногда для наглядности соединяют прямыми, получая ломаную линию. Если варьирующий признак теоретически может принимать значения меньше зарегистрированного минимального и/или больше зарегистрированного максимального, полигон замыкают на оси абсцисс в этих значениях.
В таблице представлен дискретный ряд распределения общероссийского жилого фонда по типу квартир. Полигон этого ряда представлен на рис.
Таблица
Распределение жилого фонда по типу квартир в 2008 году1
| Группы квартир по числу комнат | Количество квартир | |
| всего, млн. | в % к итогу | |
варианты, 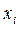 | частота, 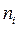 | частость, 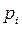 |
| 13,7 | 23,2 | |
| 23,6 | 40,0 | |
| 17,2 | 29,2 | |
| 4 и более | 4,5 | 7,6 |
| ВСЕГО | 59,0 | 100,0 |
1) по материалам статистического сборника «Российский статистический ежегодник. 2009»
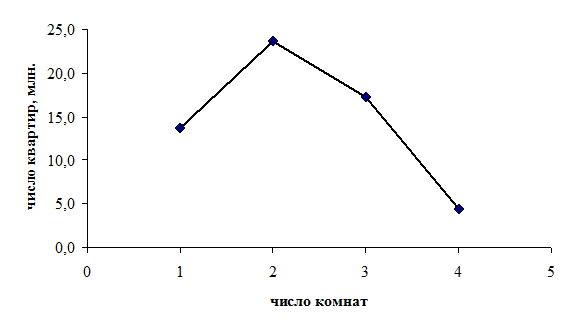
Рис. Полигон распределения жилого фонда по типу квартир в 2008 году
Гистограмма (ленточная диаграмма) – графическое изображение интервального вариационного ряда распределения, дающее представление о характере изменения его частот. При построении гистограммы по оси абсцисс откладываются величины интервалов соответстующего признака, по оси ординат – частоты, частости или плотности распределения. Для равноинтервальных рядов могут быть использованы и частоты/ частости, и плотности, для неравноинтервальных – только плотности.
Гистограмма представляет собой прямоугольники, ширина которых определяется интервалами на оси абсцисс, а высота – значениями частот, частостей или плотностей на оси ординат.
При построении графиков для дискретных или равноинтервальных рядов распределения выбор между частотами и частостями определяется необходимостью сравнения этих графиков для разных совокупностей (с различным числом наблюдений) в одной системе координат. В случае такой необходимости по оси ординат должны откладываться частости.
В таблице представлен интервальный вариационный ряд распределения населения по величине среднедушевых денежных доходов. Для правильной оценки распределения данного ряда используется характеристика плотности, т.к. ряд неравноинтервальный. Например, при оценке по частоте/частости создается впечатление, что наиболее «популярным» является интервал от 10 до 15, однако, плотность частоты/частости показывает, что в действительности таким интервалом является диапазон от 4 до 6. Гистограмма этого ряда представлена на рис.
Таблица
Распределение населения по величине среднедушевых денежных доходов в 2007 году1
| Группы населения по среднедушевому доходу, тыс.руб/мес | Численность | Величина интервала, млн.чел | Плотность распределения | ||
| всего, млн.чел | в % к итогу | абсолютная | относительная | ||
группы вариант, 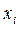 | частота, 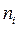 | частость, 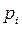 | 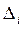 | плотность частоты, 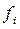 | плотность частости, 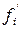 |
| до 2 | 3,7 | 2,6 | 1,8 | 1,3 | |
| 2 – 4 | 16,9 | 11,9 | 8,5 | 6,0 | |
| 4 – 6 | 21,2 | 14,9 | 10,6 | 7,5 | |
| 6 – 8 | 19,3 | 13,6 | 9,7 | 6,8 | |
| 8 – 10 | 16,1 | 11,3 | 8,0 | 5,7 | |
| 10 – 15 | 27,2 | 19,1 | 5,4 | 3,8 | |
| 15 – 25 | 23,5 | 16,5 | 2,3 | 1,7 | |
| свыше 25 | 14,4 | 10,1 | 1,4 | 1,0 | |
| ВСЕГО | 142,2 | 100,0 | - | - | - |
1) по материалам статистического сборника «Социальное положение и уровень жизни населения России. 2008»
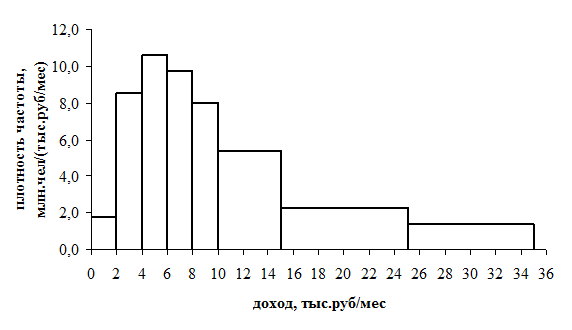
Рис. Гистограмма распределения населения по величине среднедушевых денежных доходов в 2007 году
Кумулята – графическое изображение кумулятивной кривой, дающее представление о характере изменения накопленных частот/частостей. Для построения кумуляты интервального вариационного ряда по оси абсцисс откладываются величины интервалов, а если ряд дискретный - ранжированные значения признака. По оси ординат в обоих случаях располагаются накопленные частоты или частости. Равенство или неравенство интервалов для графика кумуляты значения не имеет.
Кумулята интервального вариационного ряда представляет собой неубывающую ломаную линию, соединяющую точки пересечения концов интервалов с соответствующими им накопленными частотами. При этом соединение точек прямыми линиями обусловлено предположением о равномерном нарастании ряда накопленных частот внутри интервала. Угловой коэффициент звена кумуляты характеризует плотность распределения в соответствующем интервале: чем круче расположено звено относительно оси абсцисс, тем больше плотность в данном интервале.
В таблице представлены значения накопленного ряда для характеристики среднедушевых доходов. По этим данным построена кумулята на рис.
Таблица
Распределение населения по величине среднедушевых денежных доходов в 2007 году1
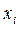 , тыс.руб/мес , тыс.руб/мес | Численность | |||
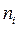 , млн.чел , млн.чел | 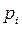 , в % к итогу , в % к итогу | накопленным итогом, млн.чел. | накопленным итогом, в % к итогу | |
накопленная частота, 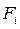 | накопленная частость, 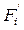 | |||
| до 2 | 3,7 | 2,6 | 3,7 | 2,6 |
| 2 – 4 | 16,9 | 11,9 | 20,6 | 14,5 |
| 4 – 6 | 21,2 | 14,9 | 41,8 | 29,4 |
| 6 – 8 | 19,3 | 13,6 | 61,2 | 43,0 |
| 8 – 10 | 16,1 | 11,3 | 77,2 | 54,3 |
| 10 – 15 | 27,2 | 19,1 | 104,4 | 73,4 |
| 15 – 25 | 23,5 | 16,5 | 127,9 | 89,9 |
| свыше 25 | 14,4 | 10,1 | 142,2 | 100,0 |
| ВСЕГО | 142,2 | 100,0 | - | - |
1) по материалам статистического сборника «Социальное положение и уровень жизни населения России. 2008»
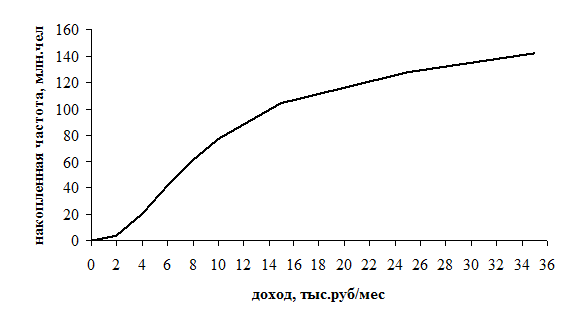
Рис. Кумулята распределения населения по величине среднедушевых денежных доходов в 2007 году
Кумулята дискретного вариационного ряда - это неубывающая, ступенчатая кривая. Строится она следующим образом. В прямоугольной системе координат отмечают точки, абсцисса которых – значение признака, ордината – накопленная частота/частость. Из точек опускают перпендикуляры на ось абсцисс. Затем из каждой точки откладывают вправо отрезок параллельный оси абсцисс до пересечения со следующим перпендикуляром.
В таблице представлены значения кумулятивного ряда для признака «число комнат в квартире». Кумулята данного ряда построена на рис.
Таблица
Распределение жилого фонда по типу квартир в 2008 году1
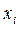 | Количество квартир | |||
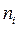 , млн. , млн. | 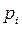 , в % к итогу , в % к итогу | накопленным итогом, млн. | накопленным итогом, в % к итогу | |
накопленная частота, 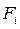 | накопленная частость, 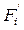 | |||
| 13,7 | 23,2 | 13,7 | 23,2 | |
| 23,6 | 40,0 | 37,3 | 63,2 | |
| 17,2 | 29,2 | 54,5 | 92,4 | |
| 4 и более | 4,5 | 7,6 | 59,0 | 100,0 |
| ВСЕГО | 59,0 | 100,0 | - | - |
1) по материалам статистического сборника «Российский статистический ежегодник. 2009»
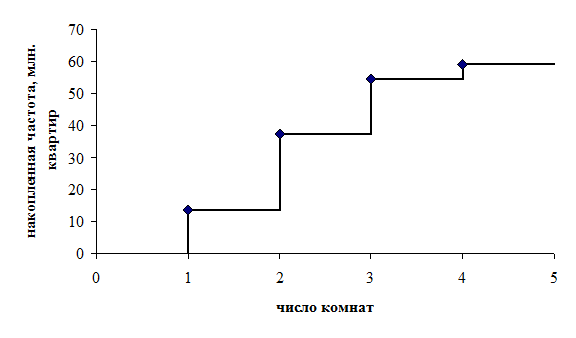
Рис. Кумулята распределения жилого фонда по типу квартир в 2008 году
Огива – это графическое изображение кумулятивной кривой, в котором оси кумуляты поменяны местами. На рис. представлена огива для распределения среднедушевого дохода.
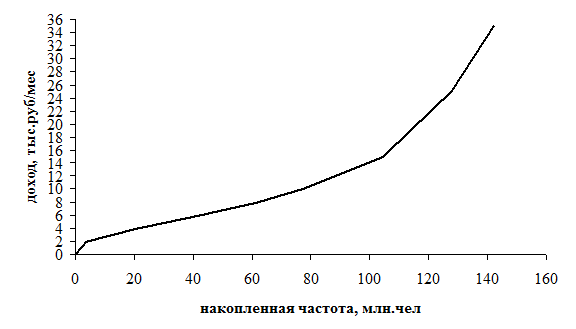
Рис. Огива распределения населения по величине среднедушевых денежных доходов в 2007 году.
Распределение единиц совокупности по групповым значениям признака – лишь одна из характеристик изучаемого явления. При сводной обработке данных каждая группа характеризуется целым набором показателей. Поэтому, наряду с построением ряда распределения, для получения комплексной оценки исследуемого явления должна быть сформирована система статистических показателей, состоящая из абсолютных, относительных и средних величин.
Контрольные вопросы
1. В чем заключается суть сводки и группировки статистических данных?
2. Каковы основные этапы сводки и группировки данных?
3. Исходя из каких соображений выбирается основание группировки и какие различия в группировках им определяются?
4. Что представляет собой сложная группировка?
5. Как определяется число групп?
6. Какие подходы существуют к определению величин интервалов группировки?
7. Назовите основные виды группировок и коротко опишите суть каждого из них.
8. Что представляет собой вторичная группировка и какими способами осуществляется?
9. Дайте определение статистической таблицы и ее основных элементов.
10. Какие правила должны выполняться при построении статистических таблиц?
11. Дайте определение ряда распределения и его основных элементов.
12. Назовите основные типы рядов распределения. На основании чего происходит их подразделение?
13. Дайте определение статистического графика.
14. Какие графики строятся для отображения изменения частот вариационного ряда?
15. Что представляют собой кумулята и огива и как они строятся?
 2015-04-12
2015-04-12 54673
54673
