 Пограничный слой атмосферы - нижний слой атмосферы вертикальной продолжительностью от нуля до 1,5-2 км, в пределах которого турбулентный обмен развит даже внутри однорядных воздушных масс. В этом слое необходимо учитывать силу турбулентного трения. Рассмотрим модель стационарного горизонтального однородного пограничного слоя с априорио заданным профилем коэффициента турбулентности. Условия стационарности и горизонтальной однородности пограничного слоя позволяют считать, что составляющая скорости u и v в движущейся воздушной массе в единицу времени не изменяется, т. е. левые части первого и второго уравнения движения равны нулю.
Пограничный слой атмосферы - нижний слой атмосферы вертикальной продолжительностью от нуля до 1,5-2 км, в пределах которого турбулентный обмен развит даже внутри однорядных воздушных масс. В этом слое необходимо учитывать силу турбулентного трения. Рассмотрим модель стационарного горизонтального однородного пограничного слоя с априорио заданным профилем коэффициента турбулентности. Условия стационарности и горизонтальной однородности пограничного слоя позволяют считать, что составляющая скорости u и v в движущейся воздушной массе в единицу времени не изменяется, т. е. левые части первого и второго уравнения движения равны нулю.
Примем коэффициент турбулентности равным некоторому среднему для пограничного слоя значению. Запишем уравнения движения:
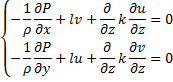
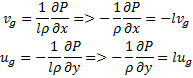
Учтём k =const:
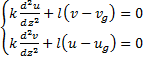 -система уравнений Экмана-Акнерблома
-система уравнений Экмана-Акнерблома
Граничные условия:
z=0; u=0; v=0
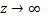 ;
; 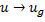 ;
; 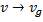
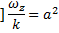
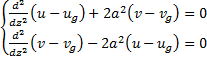
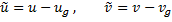
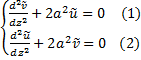 Домножим (1) на
Домножим (1) на 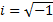 и сложим с (2)
и сложим с (2)
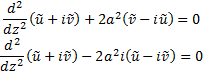
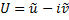
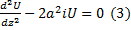
Перепишем граничные условия
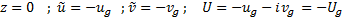
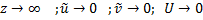
Запишем характеристические уравнения
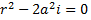
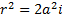
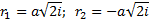
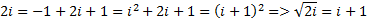
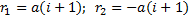
Решение дифференциального уравнения (3) имеет вид:
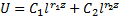
Определим произвольные постоянные 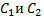 из граничных условий
из граничных условий
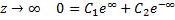
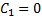
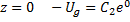
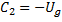
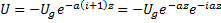
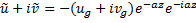
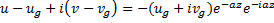
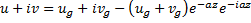
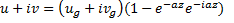
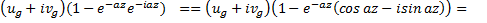
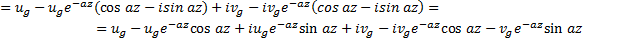
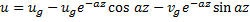
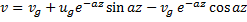
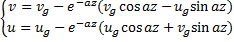
Направим ось x по геострофическому вектору, тогда 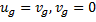
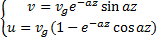 (4)
(4)
Годограф вектора, описываемый соотношениями (4) представляет собой логарифмическую спираль, которая называется спиралью Экмана. Проанализируем полученное решение.
1) 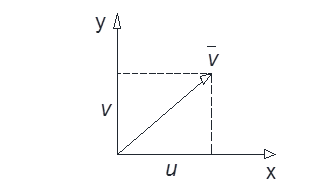 Найдём высоту, на которой ветер впервые совпал по направлению с геострофическим.
Найдём высоту, на которой ветер впервые совпал по направлению с геострофическим.
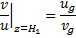
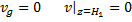
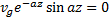
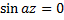
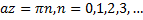
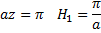
2) Найдём высоту, где ветер впервые по модулю совпал с геострофическим. Будем исходить из того, что если совпадают модули, то совпадают и квадраты модулей.
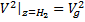
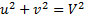
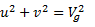
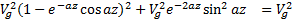
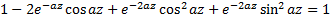
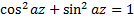
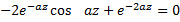
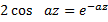
Имеем трансцендентное уравнение
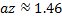

3) Найдём высоту,где модуль скорости ветра
впервые достигает максимума.
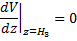
Для удобства снова будем рассматривать квадрат модуля.
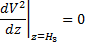
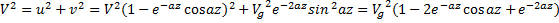
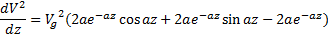
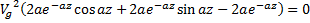
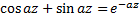
Вспомним из прямоугольной тригонометрии формулу: 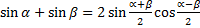
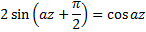
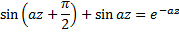
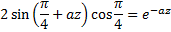
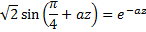
Снова имеем трансцендентное уравнение, решив которое приближенно получим высоту 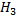 .
.
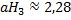
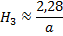
Получается, что ветер в пограничном слое сначала совпадает с геострофическим по модулю, а затем достигает максимального значения и, наконец, совпадает с геострофическим по направлению. Оценим высоту пограничного слоя, приняв за его границу высоту, где ветер впервые совпадает по направлению с геострофическим. 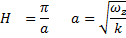
Пусть:
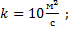
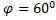
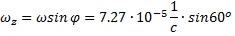
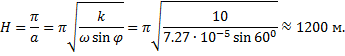
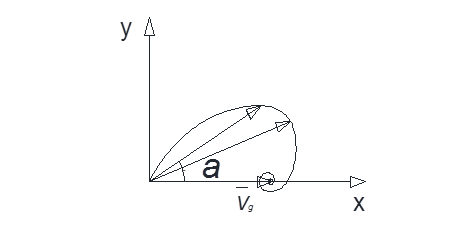 Изобразим спираль Экмана.
Изобразим спираль Экмана.
α-угол поворота ветра в пограничном слое
оценим максимальный угол поворота ветра по модели Экмана.
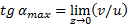
Имеем неопределённость вида 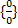
Эту неопределенность раскроем по правилу Лопиталя.
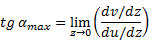
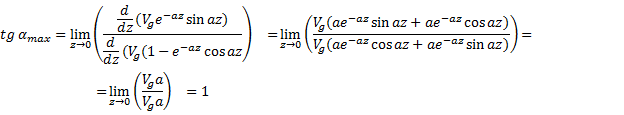
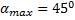
Реальные значения 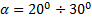
 2015-08-12
2015-08-12 3360
3360