Пограничный слой. Характеристики пограничного слоя

Возможность практического использования модели вязкой жидкости открылась благодаря тому, что действие вязкости проявлялось в узкой области вблизи граничной поверхности. В самом деле, из-за прилипания жидкости на поверхности тела обтекания скорость равна нулю. Следовательно, вблизи поверхности число Рейнольдса 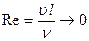. Это означает, что непосредственно у обтекаемой поверхности, где 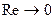, вязкость 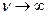играет наиболее существенную роль по сравнению с областью течения, удаленной от тела.

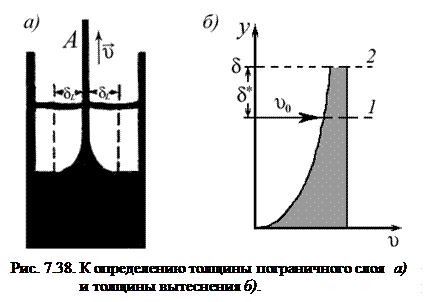
На рис. 7.38 а изображено, как пластинка медленно вытягивается вверх из наполненного глицерином стеклянного сосуда. Если перед началом опыта нижнюю часть глицерина, а также расположенные выше него слои окрасить в разные цвета (получим горизонтальные окрашенные поверхности глицерина), то во время движения поверхности с обеих сторон пластинки искривляются внутри широкой области. При этом частички жидкости испытывают вращение, справа – по часовой стрелке, слева – против. В такой области влияние сил вязкости значительно.

Зона влияния вязкости образует относительно тонкий слой, называемый пограничным слоем (погранслоем). Самая внутренняя часть пограничного слоя прилипает к твердому телу и движется с такой же скоростью, как и само тело. Вне погранслоя влияние вязкости мало и жидкость в этой области течения можно считать невязкой. Градиенты скорости по нормали к поверхности тела в погранслое, в большинстве случаев, не малы. Поэтому поверхностные напряжения и силы вязкого трения со стороны погранслоя на тело могут принимать достаточно большие значения, несмотря на его относительную тонкость. Движение жидкости в погранслое может быть как ламинарным, так и турбулентным. Переход между режимами может происходить в пределах длины тела обтекания (например, в носовой части тела погранслой ламинарный, но уже на корме он может стать турбулентным). Различают пристеночные пограничные слои. Они проявляются в струйном течении и в следе за обтекаемым телом. Расчет динамических параметров погранслоя представляет интерес в связи с определением силовых воздействий вязкой жидкости на движущееся судно.

Толщина пограничного слоя – величина неопределенная. Она отсчитывается от стенки в направлении поперек потока до некоторого расстояния. Толщину погранслоя условно принимают равной такому расстоянию от поверхности, на котором скорость отличается от скорости потенциального внешнего обтекания на .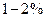

Толщину пограничного слоя можно оценить на основе следующих рассуждений. Пусть жидкость в пограничном слое имеет поперечное сечение 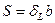(– ширина слоя, – толщина слоя) и проходит за время путь 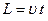. Количество жидкости, протекающей при этом через поперечное сечение 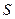за время , имеет массу 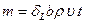и несет импульс 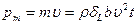. Отношение 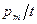должно быть равно силе 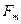, которая поддерживает скорость течения 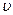. Сила 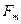может быть записана (см. § 9) как

.

Приравнивая выражения для 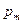и , получим:

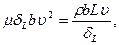
а отсюда – выражение для толщины пограничного слоя

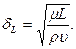(7.108)

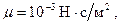
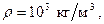
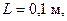
Например, для воды на основе (7.108) при 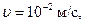имеем .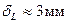

Более точное и конкретное определение толщины пограничного слоя в гидромеханике связывается с двумя характеристиками пограничного слоя:

– толщиной вытеснения

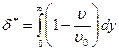; (7.109)

– толщиной потери импульса

. (7.110)

Здесь – скорость внешнего обтекания.

Для определения толщины вытеснения сравнивается местоположение линий тока, т.е. линий равных расходов двух пограничных слоев: одного слоя, который состоит как бы из идеальной жидкости, и другого, состоящего из вязкой жидкости.

В погранслое с идеальной (невязкой) жидкостью линия тока 1, отвечающая некоторому расходу через поперечное сечение между стенкой и этой линией тока, располагается ближе к стенке, чем линия тока 2 в погранслое с реальной (вязкой) жидкостью и расходом (рис. 7.38 б). Из-за вязкости при приближении к стенке поток замедляется и для сохранения расхода сечение должно быть больше, чем в идеальном погранслое. Размер зоны вытеснения равен величине смещения 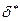– линии тока реальной жидкости по отношению к линии тока идеальной жидкости. Величину смещения 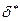находим из условия равенства двух расходов:

(7.111)

Используем тождество

Добавим в обе части равенства член 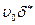, в результате получим

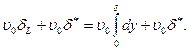
Из последней формулы находим

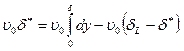
Подставляя сюда условие равенства двух расходов (7.104), имеем:

Интегральная толщина вытеснения содержит сходящийся интеграл в силу асимптотического стремления 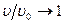при . Поэтому верхний предел можно заменить с на . На рис. 7.38 б заштрихованная площадь, равная интегралу (7.111), не зависит от точности определения толщины погранслоя . Толщина вытеснения 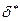– кинематическая характеристика пограничного слоя.

Толщиной потери импульса пограничного слоя называется величина, характеризующая динамическое влияние вязкости на сопротивление. Кроме толщины вытеснения и толщины потери импульса, в пограничном слое вводится величина их отношения 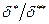, называемая формпараметром. Как показывает практика, в пограничном слое формпараметр можно считать величиной постоянной.

Итак, вблизи граничных поверхностей выделяют две области: область пограничного слоя потока, где необходимо учитывать вязкость, и область ядра потока, в которой течение можно считать невязким. На границе соприкосновения этих зон решения, полученные для вязкого и невязкого течения, должны совпадать.

Вычисления показывают, что пограничный слой при обтекании криволинейной поверхности испытывает отрыв. Отрыв имеет место в диффузорной части потока там, где давление по потоку уменьшается. Такой же характер движения жидкости с отрывом пограничного слоя получается и в случае турбулентного обтекания криволинейной поверхности с произвольным профилем скорости.

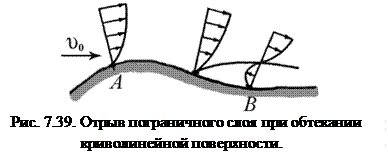Картина распределения скоростей в пограничном слое в этом случае изображена на рис. 7.39, где показано обратное по отношению к набегающему потоку течение в пограничном слое, приводящее к его срыву. В конфузорной части потока (точка на рис. 7.39) отрыв слоя невозможен. Здесь . Снижающееся вдоль по потоку давление способствует движению частиц в пограничном слое по направлению внешнего потока.

В диффузорной части потока (точка 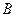на рис. 7.39) 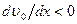и . Частицы жидкости, попадающие в эту область пограничного слоя, притормаживаются за счет роста давления вдоль стенки. В непосредственной близости от поверхности, где скорости малы, противодействующий потоку градиент давления способствует обратному движению и возникновению завихрения потока. Возникающие вихри отрываются от тела, образуя вихревую дорожку. Образование в следе за обтекаемым телом вихрей приводит к дополнительному вихревому сопротивлению. В этом случае потенциальный поток идеальной жидкости вне пограничного слоя не может моделироваться картиной плавного обтекания и должен быть заменен какой-либо другой схемой. Например, может быть принята схема струйного течения или схема обтекания тела системой вихрей за ним. Такие вихри наблюдаются в природе и могут рассматриваться как результат действия вязкости жидкости в области пограничного слоя, т.к. завихренность срывающегося пограничного слоя и приводит к образованию вихрей.

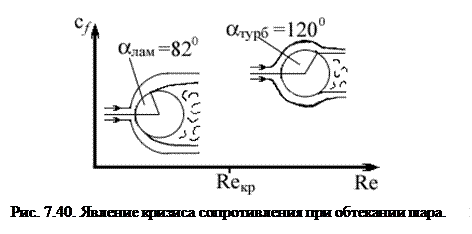Поскольку градиент давления зависит от формы тела, то вихревое сопротивление изменяется с изменением формы обтекаемых тел. Хорошо обтекаемые тела – это тела с относительно большим удлинением, т.е. у которых отношение продольного размера к поперечному размеру больше единицы. К одному из типов плохо обтекаемых тел относится шар. Из-за малого удлинения градиент давления вдоль поверхности значителен. В зависимости от числа Рейнольдса место отрыва смещается от миделя к корме (рис. 7.40).

Вихревая зона по мере роста скорости набегающего на шар потока сужается, и общее сопротивление падает. Явление резкого снижения сопротивления плохо обтекаемых тел с перемещающимися точками отрыва пограничного слоя при переходе от ламинарного к турбулентному режиму течения называется кризисом сопротивления. Кризис сопротивления зависит от степени турбулентности набегающего потока.