Интегральные соотношения пограничного слоя

Интегральные соотношения пограничного слоя выводятся либо аналитически путем интегрирования системы дифференциальных уравнений пограничного слоя, либо из физических соображений путем применения интегральных законов сохранения к жидкому элементу, принадлежащему пограничному слою.

Остановимся на первом подходе. Предварительно преобразуем первое уравнение системы (2.132) к виду, удобному для дальнейшего анализа.

С этой целью запишем сначала систему (2.132) в виде

;

,

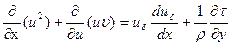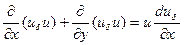а затем вычтем из второго уравнения первое. Тогда получим

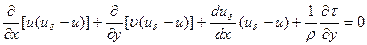. (2.133)

Умножим левую часть (2.133) на произведение 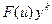, где F(u) — произвольная дифференцируемая функция, k=0, 1, 2..., и проинтегрируем полученное выражение по у в пределах пограничного слоя. Если рассматривается асимптотический пограничный слой, то интегрирование должно осуществляться от 0 до бесконечности. Если же рассматривается пограничный слой конечной толщины 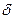, то интегрирование должно производиться от 0 до 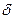. В дальнейшем верхние пределы интегралов будут обозначаться двояко, отражая то или иное понимание пограничного слоя.

Итак, получаем исходное интегральное соотношение

+++ .

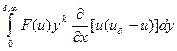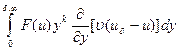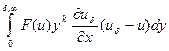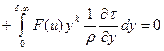При 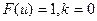получаем

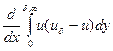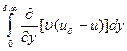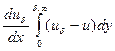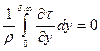+++ (2.134)

Второй интеграл равен нулю. Введем обозначения интегральных характеристик пограничного слоя:

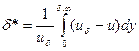- толщина вытеснения; (2.135)

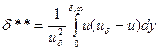- толщина потери импульса. (2.136)

Толщина вытеснения 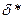характеризует отклонение линий тока от поверхности обтекаемого тела вследствие существования пограничного слоя. Наглядное представление об этом дает схема обтекания пластины (рис. 2.6).

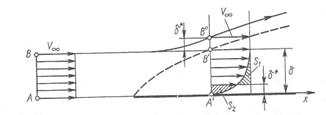Рис.2.6 Пограничный слой

Расход жидкости через сечение АВ равен . В сечении А'В' скорости u(у) переменны. Они изменяются от нуля до 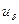. Следовательно, расход жидкости через сечение А'В' меньше, чем через сечение АВ. Дополним профиль скорости до однородного, положив 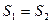. Тогда, приравняв расходы в сечении АВ и А'В", получаем очевидный вывод, что точка В", через которую проходит линия тока, должна быть смеще­на вверх на толщину вытеснения 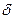*. Проведенное рассуждение подчеркивает также, что граница пограничного слоя не является линией тока.

Сходным образом можно интерпретировать и толщину потери импульса.

При использовании (2.135) и (2.136) интегральное соотноше­ние импульсов приобретает вид

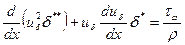(2.137)

или

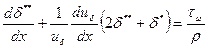(2.138)

Обычно употребляются следующие параметры:

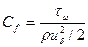-местный коэффициент трения;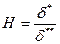-формпараметр. Тогда уравнению (2.138) можно придать общеизвестный вид:

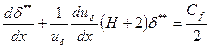(2.139)

Целесообразность использования форм параметра H диктуется тем, что он изменяется незначительно, и в определенных случаях для получения приближенных решений допустимо считать его постоянным.

При F(u)=u, k=0 получим уравнение кинетической энергии, часто называемое просто уравнением энергии:

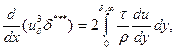(2.140)

где δ***==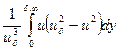 - толщина потери энергии. Действуя аналогичным образом, можно получить другие формы инте­гральных соотношений.

Подчеркнем одно важное обстоятельство. Во всех выкладках фигурирует понятие напряжения трения безотносительно к виду течения: ламинарному или турбулентному. Следовательно, полу­чаемые итоговые уравнения будут справедливы и для ламинар­ного и для турбулентного пограничного слоя.