Для улучшения свойств алгоритма оптимальной интерполяции используется общий алгоритм, в котором учитывается статистика прямой задачи [1].
Если имеется трехмерная модельная сетка с 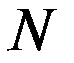 станций измерений и
станций измерений и 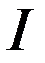 узлов модельной сетки, то стоит задача получения значений
узлов модельной сетки, то стоит задача получения значений 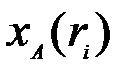 , где
, где 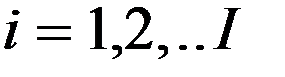 , основываясь на результатах измерений
, основываясь на результатах измерений 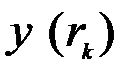 , где
, где 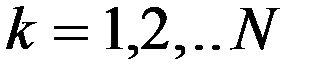 . Оценки нормы имеются только в узлах модельной сетки, как модельный прогноз. Тогда прямая задача определяется как представление нормы в точках измерений:
. Оценки нормы имеются только в узлах модельной сетки, как модельный прогноз. Тогда прямая задача определяется как представление нормы в точках измерений:
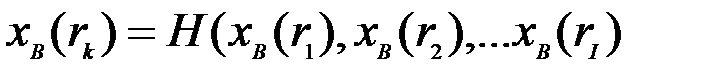 .
.
Если предположить, что используется линейный алгоритм интерполяции, то
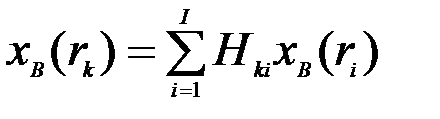 ,
,
где 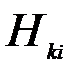 представляют собой веса прямой задачи, т.е. интерполяции.
представляют собой веса прямой задачи, т.е. интерполяции.
Тогда известный метод представления анализируемого значения метеовеличины 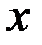 можно записать в виде
можно записать в виде
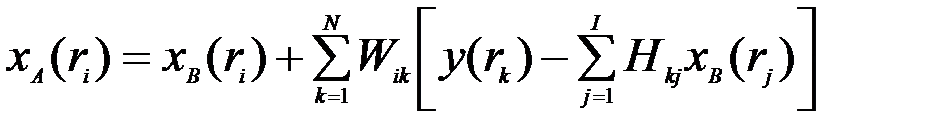
или в матричном виде
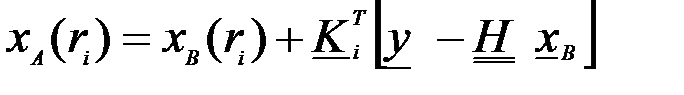 ,
,
где 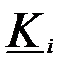 - вектор размерности
- вектор размерности 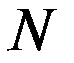 , содержащий апостериорные веса
, содержащий апостериорные веса 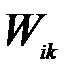 ,
,
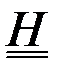 - матрица размерности
- матрица размерности 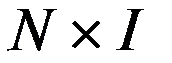 , содержащая коэффициенты интерполяции,
, содержащая коэффициенты интерполяции,
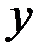 и
и 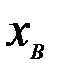 - вектора размерности
- вектора размерности 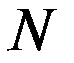 и
и 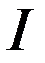 , содержащие значения измерений и оценки нормы или первого приближения для модели.
, содержащие значения измерений и оценки нормы или первого приближения для модели.
Минимизируя по отношению к весам, получаем:
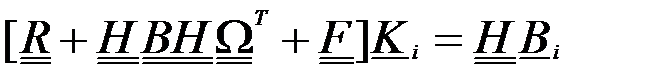
где 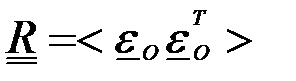 матрица ковариаций ошибок измерений, размерности
матрица ковариаций ошибок измерений, размерности 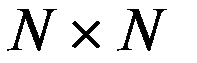 ,
,
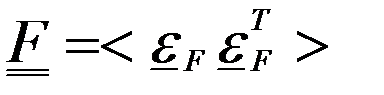 - матрица ошибок интерполяции, размерности
- матрица ошибок интерполяции, размерности 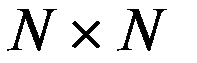 ,
, 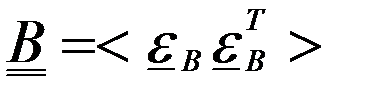 - матрица ошибок оценивания нормы, размерности
- матрица ошибок оценивания нормы, размерности 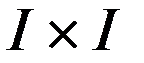 ,
, 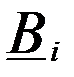 - вектор ковариаций ошибок представления нормы, размерности
- вектор ковариаций ошибок представления нормы, размерности 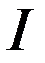 .
.
Это уравнение позволяет получить веса для 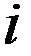 -го узла модельной сетки.
-го узла модельной сетки.
Для всей модельной сетки:
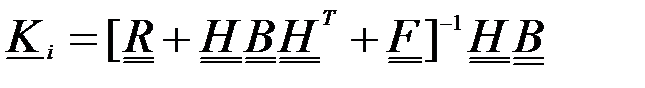 ,
,
а уравнение для поправок в узлах модельной сетки
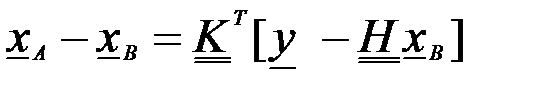 .
.
 2015-08-21
2015-08-21 472
472








