2015-08-21
1536
Краткая теория
Одномерное тело (бесконечные пластина и цилиндр, шар) с одинаковой температурой во всех точках, равной t/, в начальный момент времени τ0 погружается в жидкость с неизменной температурой tж. Коэффициент теплоотдачи на поверхности тела (для пластины с обеих боковых сторон) одинаков и постоянен.
Если за начало отсчета температуры принять температуру окружающей среды tж и избыточную температуру стенки обозначить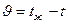 
то дифференциальное уравнение теплопроводности для твердых тел:
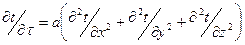, (1)
а при рассмотрении относительно только одной координаты принимает вид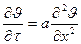 
Граничные условия: при х = ±δ
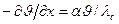
Начальное условие: при τ = 0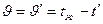 
При этом температуры тела на поверхности tс и в плоскости симметрии t0 для любого момента времени определяются из следующих соотношени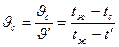й:
и
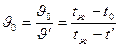
где t/ - начальная температура по всему сечению тела.
Пример распределения температур по толщине плоской стенки во времени
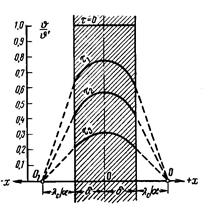
Рис. 2. Изменение температурного поля в плоской неограниченной стенке
от времени при охлаждении.
|
|
|
Безразмерная температура тела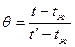 
является функцией безразмерной координаты 
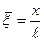, числа Био 
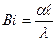и числа Фурье 
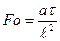, где х - текущая координата в направлении теплового потока, м; ℓ-характерный линейный размер тела, м; λ – коэффициент теплопроводности, Вт/м·К и а = 
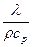- коэффициент температуропроводности материала тела, м2/с.
Аналитическое решение уравнения теплопроводности при заданных начальных и граничных условиях запишется:
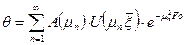(2)
Здесь А и U – некоторые функции от корней характеристических уравнений μn, а сами корни являются однозначной функцией критерия Био.
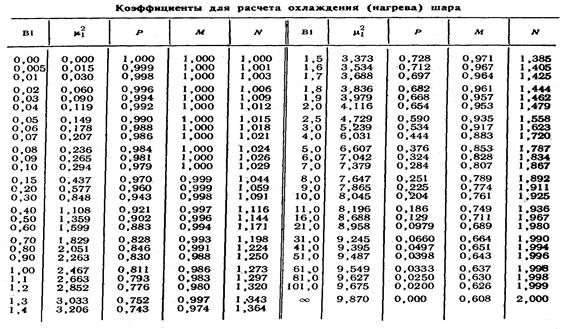
Таблица 1.
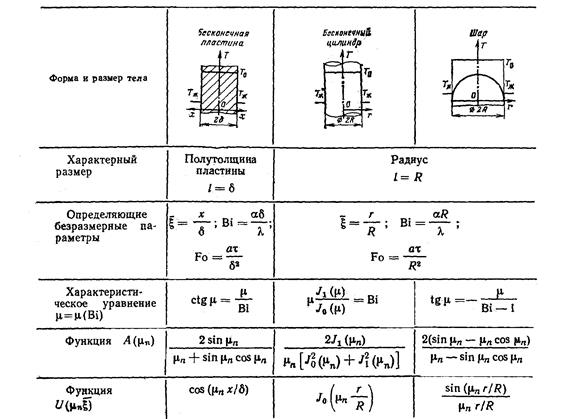
В таблице 1 приведены: вид характеристических уравнений и соотношения для расчета функций А(μn) и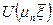 
для случая охлаждения (нагрева) бесконечной пластины, бесконечного цилиндра и шара. Через J0 и J1 обозначены функции Бесселя первого рода нулевого и первого порядка (функции приведены в табл.2). Начало координат расположено на средней плоскости для пластины, на оси для цилиндра и в центре для шара. Решение (2) может быть использовано для бесконечной пластины в случае, если одна из боковых плоскостей имеет абсолютную теплоизоляцию. В этом случае начало координат необходимо поместить на теплоизолированной стенке и в качестве характерного размера принять всю толщину стенки 2δ.
Первые шесть корней характеристических уравнений из таблицы 1 приведены в таблицах №№ 2 – 5.
При Fo>0,3 ряд (2) оказывается настолько быстро сходящимся, что для практических целей достаточно ограничиться первым членом (с погрешностью не выше 1%).
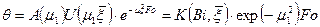(3)
Так для плоской пластины общий вид решения
|
|
|
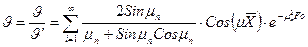(3а)
а для практических целей решение записывается
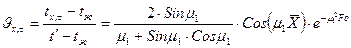(3/а)
Здесь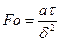 
, 
, 
, 
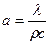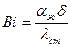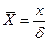
Координата точки О на оси х расположена на расстоянии λст/αж, м.
Для расчетов применяют вспомогательные таблицы, включающие так называемые частные корни решения характеристического уравнения, обозначаемые обычно μ. Как отмечено выше, точное решение содержит набор частных решений, отличающихся значениями корней решения μn. Выше отмечено, что для практических целей применяют уравнения (3), включающие только первый член с коэффициентом μ1. Само значение μ1 зависит от критерия Bi и приводится в специальных таблицах.
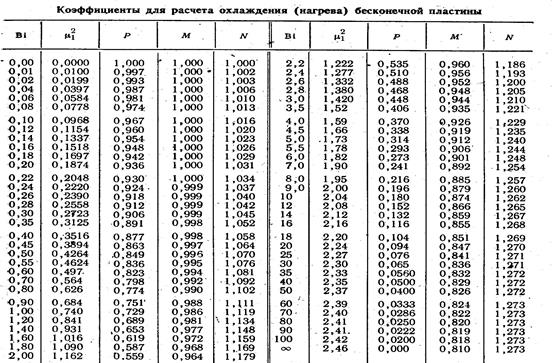
Произвести расчет безразмерной температуры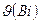 
в четырех точках с координатами 
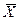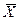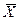=0, 1/3, 2/3 и 1,0 для следующих значений Bi 0,01, 0,05, 0,1, 0,5, 1,0, 5 и 10, Fo в зависимости от варианта и построить график безразмерных температур по Био для =0 и =1
Варианты заданий для расчета
| Fo =20 | Fo=30 | Fo= 50 |
