Як уже відзначено вище, при алгебраїчній інтерполяції функція, що інтерполює, шукається у вигляді багаточлена, він називається інтерполяційним багаточленом. Задача його знаходження формулюється в такий спосіб.
Дано значення 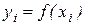 функції функції 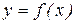 в різних вузлових крапках х0, х1, …хn. Необхідно знайти багаточлен Pn(x) ступеня n, що приймає у вузлових точках задані значення. в різних вузлових крапках х0, х1, …хn. Необхідно знайти багаточлен Pn(x) ступеня n, що приймає у вузлових точках задані значення.
|
Виявляється, що дана задача розв'язна й має єдине рішення. Дійсно, нехай
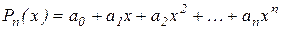 ,
,
– шуканий багаточлен, 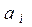 – невідомі коефіцієнти.
– невідомі коефіцієнти.
Тоді для визначення коефіцієнтів 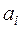 маємо лінійну систему рівнянь
маємо лінійну систему рівнянь
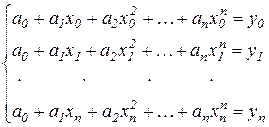 (2.1) (2.1)
|
Головним визначником системи (2.1), позначимо його через 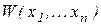 , є визначник
, є визначник
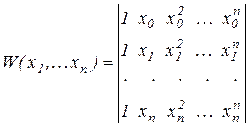 ,
,
який називається визначником Вандермонда.
Індукцією по n можна показати, що
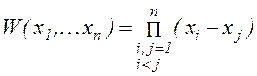 .
.
Очевидно, що при 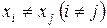 значення
значення 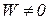 . Отже, система (2.1) має єдине рішення й, отже, існує єдиний інтерполяційний багаточлен.
. Отже, система (2.1) має єдине рішення й, отже, існує єдиний інтерполяційний багаточлен.
 2015-08-21
2015-08-21 329
329








