Він шукається у вигляді
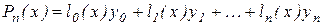 (2.2) (2.2)
|
де коефіцієнти 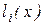 є багаточленами й задовольняють умовам
є багаточленами й задовольняють умовам
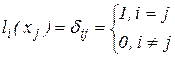 .
.
Виявляється, що цих вимог досить для однозначного визначення 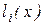 . Дійсно, багаточлен
. Дійсно, багаточлен 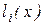 звертається в нуль у вузлових точках
звертається в нуль у вузлових точках 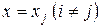 . Отже, він має розкладання
. Отже, він має розкладання
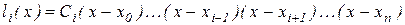 .
.
Покладемо тепер 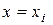 . Тоді
. Тоді
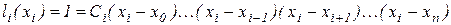 ,
,
звідки
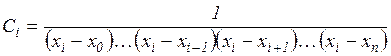 .
.
З метою скорочення запису введемо функцію
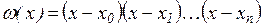 , (2.3) , (2.3)
|
тоді
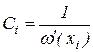 ,
,
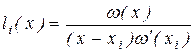
і багаточлен (2.2) приймає вид
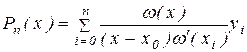 , (2.4) , (2.4)
|
де ω(x) описується вираженням (2.3). Багаточлен (2.4) і називається інтерполяційним багаточленом Лагранжа.
 2015-08-21
2015-08-21 340
340








