За аналогією з (2.6) розглянемо багаточлен ступеня n.
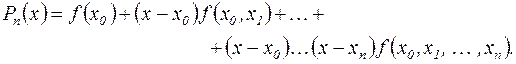 (2.7) (2.7)
|
Визначимо його значення у вузлових точках. Так, безпосередньо з (2.7) маємо
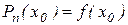
Далі,
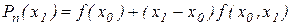 ,
,
але, з урахуванням (2.6) при 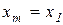 це рівняється
це рівняється 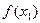 .
.
Т.о.
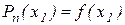
Аналогічним образом одержуємо, що
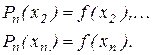
Таким чином, багаточлен (2.7) приймає задані значення в заданих точках і, отже, є інтерполяційним. Він і називається інтерполяційним багаточленом Ньютона. Помітимо, що в силу одиничності (п. 2.2) розходження між інтерполяційними багаточленами Лагранжа й Ньютона чисто зовнішні.
 2015-08-21
2015-08-21 383
383








