Кінцеві й розділені різниці відіграють особливу роль у теорії інтерполяції. Вони використовуються як для формування нових інтерполяційних формул, так і для оцінки погрішності інтерполяції.
Нехай дана таблиця 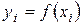 значень функції
значень функції 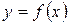 . Кінцевою різницею першого порядку в точцi xi (позначається символом
. Кінцевою різницею першого порядку в точцi xi (позначається символом 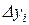 ), називається вираження
), називається вираження
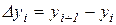 ,
,
другого порядку, позначається 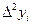 , – вираження
, – вираження
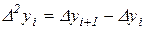 ,
,
k-го порядку, –
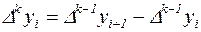 . . |
Так, наприклад, 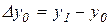 ,
, 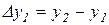 ,
, 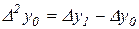
Розділеною різницею першого порядку в точках 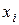 ,
, 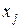 , позначається
, позначається 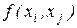 , називається вираження
, називається вираження
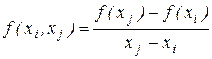 ,
,
другого порядку в точках 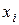 ,
, 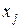 ,
, 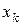 , позначається
, позначається 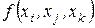 , – вираження
, – вираження
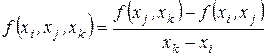 ,
,
k-го порядку в точках 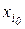 ,
, 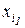 ,
, 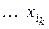 , – вираження
, – вираження
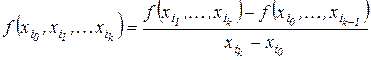 .
.
Так, наприклад,
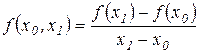 ,
,
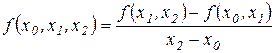 ,
,
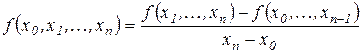 .
.
Одержимо деякі корисні для подальшого співвідношення, пов'язані з розділеними різницями.
Виразимо 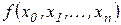 через значення функції у вузлових точках. Так, безпосередньо з визначення треба
через значення функції у вузлових точках. Так, безпосередньо з визначення треба
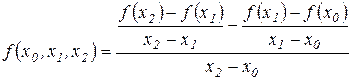 ,
,
і, після очевидних перетворень,
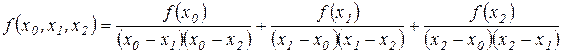 .
.
Продовжуючи, далі, по індукції, одержимо
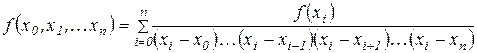 .
.
Або, для скорочення запису, використовуючи функцію 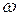 (2.3),
(2.3),
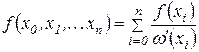 (2.5) (2.5) |
Зауваження. Якщо в 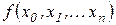 поміняти місцями значення поміняти місцями значення 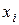 , то це приведе лише до перестановки відповідних доданкiв правої частини співвідношення (2.5). Отже, розділені різниці є симетричними функціями вузлових точок. , то це приведе лише до перестановки відповідних доданкiв правої частини співвідношення (2.5). Отже, розділені різниці є симетричними функціями вузлових точок. |
Так, наприклад
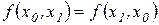 ,
,
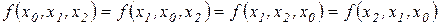 і т.д.
і т.д.
Одержимо тепер друге корисне співвідношення.
Виразимо 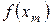 через розділені різниці. Так, безпосередньо з визначення треба
через розділені різниці. Так, безпосередньо з визначення треба
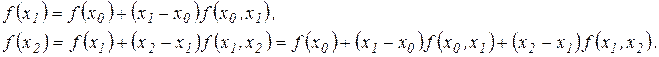
Додаючи тепер до правої частини 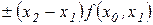 після очевидних перетворень одержимо
після очевидних перетворень одержимо
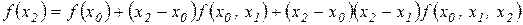 .
.
Міркуючи далі по індукції по m прийдемо до шуканого співвідношення
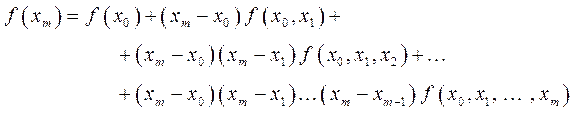 (2.6) (2.6) |
Якщо тепер змінити нумерацію точок і позначити 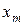 через
через 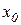 ,
, 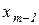 через
через 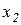 і т.д., то співвідношення (2.6) з урахуванням симетричності розподілених різниць приймає вид
і т.д., то співвідношення (2.6) з урахуванням симетричності розподілених різниць приймає вид
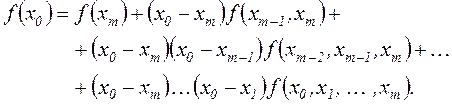 (2.61) (2.61) |
 2015-08-21
2015-08-21 781
781








