Дифференциал функции.
Пусть функция 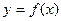 дифференцируема на отрезке
дифференцируема на отрезке 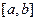 . Производная этой функции в некоторой точке
. Производная этой функции в некоторой точке 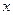 отрезка
отрезка 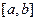 определяется равенством
определяется равенством 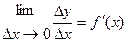 . Отношение
. Отношение 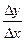 при
при 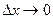 стремится к определенному числу
стремится к определенному числу  и, следовательно, отличается от производной
и, следовательно, отличается от производной  на величину бесконечно малую:
на величину бесконечно малую: 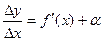 , где
, где 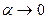 при
при 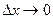 . Умножая все члены последнего равенства на
. Умножая все члены последнего равенства на 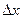 , получим:
, получим: 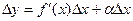 , где
, где 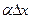 - бесконечно малая величина. Произведение
- бесконечно малая величина. Произведение 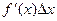 называют дифференциалом функции и обозначают через
называют дифференциалом функции и обозначают через 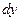 или
или 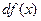 . Если функция
. Если функция 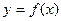 имеет производную
имеет производную  в точке
в точке 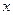 , то произведение производной
, то произведение производной  на приращение
на приращение 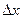 аргумента называется дифференциалом функции и обозначается символом
аргумента называется дифференциалом функции и обозначается символом 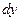 :
:
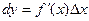 или
или 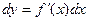 (6)
(6)
Производные высших порядков. Пусть функция 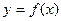 дифференцируема на некотором отрезке
дифференцируема на некотором отрезке 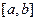 . Значение производной
. Значение производной  зависят от
зависят от 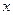 . Дифференцируя эту функцию, мы получаем так называемую вторую производную от функции
. Дифференцируя эту функцию, мы получаем так называемую вторую производную от функции 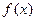 . Производная от первой производной называется производной второго порядка от первоначальной функции и обозначается символом
. Производная от первой производной называется производной второго порядка от первоначальной функции и обозначается символом 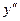 или
или 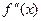 .
.
Производная от второй производной называется производной третьего порядка и обозначается через 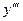 или
или 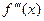 .
.
Производной 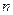 -го порядка от функции
-го порядка от функции 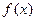 называется производная от производной
называется производная от производной 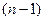 -го порядка и обозначается символом
-го порядка и обозначается символом 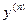 или
или 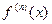 :
: 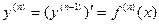 .
.
Пусть 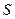 , пройденный поступательно движущимся телом, в зависимости от времени
, пройденный поступательно движущимся телом, в зависимости от времени 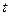 выражается формулой
выражается формулой 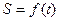 ; Как известно,
; Как известно, 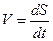 . Ускорением в данный момент называется предел отношения приращения скорости к приращению времени, когда последнее стремится к нулю:
. Ускорением в данный момент называется предел отношения приращения скорости к приращению времени, когда последнее стремится к нулю: 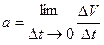 или
или 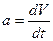 но, так как
но, так как 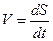 то
то
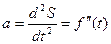 , т.е. ускорение прямолинейного движения равно второй производной от пути по времени.
, т.е. ускорение прямолинейного движения равно второй производной от пути по времени.
Задание на СРС:
1. Основные теоремы дифференциального исчисления (Ролля (корни производной), Лагранжа (конечные приращения), Коши (отношения приращения)).[1,2-с.163]
2. ИДЗ-стр.291-299, № 4-7.[3] (Срок сдачи по графику)
Задание на СРСП:
1. Правило Лопиталя.Формула Тейлора и Маклорена [1,2]
Контрольные вопросы:
- Производные неявной функции.
- Производные функции, заданной параметрически.
- Касательная к кривой; Нормаль к кривой.
- Дифференциал функции.
Задачи:
№1. Найти 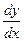 , если: а)
, если: а) 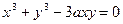 Ответ:
Ответ: 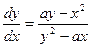 .
.
б) 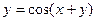 Ответ:
Ответ: 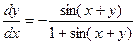 .
.
№2. Найти 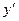 , если:
, если:
а) 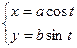 Ответ:
Ответ: 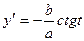 .
.
б) 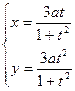 Ответ:
Ответ: 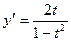 .
.
№3. Найти тангенсы углов наклона касательных к кривым: 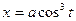 ,
, 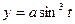 при
при 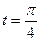 . Сделать чертеж. Ответ:-1.
. Сделать чертеж. Ответ:-1.
№4. Найти дифференциалы функции:
а) 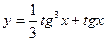 Ответ:
Ответ: 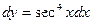
б) 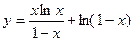 Ответ:
Ответ: 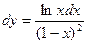
№5. Найти производные третьего порядка
а) 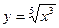 Ответ:
Ответ: 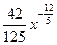
б) 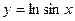 Ответ:
Ответ: 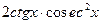
№6. Написать уравнение касательной и нормали к кривой 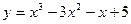 в точке
в точке 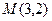 Ответ: Касательная
Ответ: Касательная 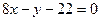 ; нормаль
; нормаль 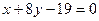 .
.
№7. Дана функция 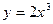 . Найти dy -?
. Найти dy -?
№8. Дана функция 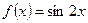 . Найти
. Найти 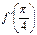 .
.
 2015-08-21
2015-08-21 331
331








