Матрицей размера 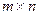 называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются заглавными буквами латинского алфавита, например A, B, C, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 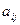 , где i-номер строки, j-номер столбца.
, где i-номер строки, j-номер столбца.
Например, матрица 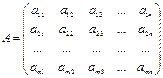
или матрица A=(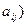 , i=1,2, 3, …m, j=1, 2,3,…n.
, i=1,2, 3, …m, j=1, 2,3,…n.
Матрица, состоящая из одной строки, называется матрицей строкой, а из одного столбца – матрицей столбцом: A=(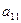
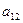
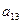 …
… 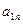 ) – матрица-строка. Матрица называется квадратной n-го порядка, если m=n.
) – матрица-строка. Матрица называется квадратной n-го порядка, если m=n.
Элементы матрицы 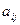 у которых i=j, называются диагональными и образуют главную диагональ матрицы.
у которых i=j, называются диагональными и образуют главную диагональ матрицы.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, остальные нули, то матрица называется единичной и обозначается Е.
Произведением матрицы А на число λ называется матрица В=λА, элементы которой 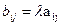 , для
, для 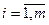 ,
, 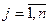 .
.
Суммой двух матриц А и В одинакового размера mxn называется С=А+В, элементы которой 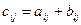 для
для 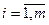 ,
, 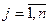 (т.е. матрицы складываются поэлементно).
(т.е. матрицы складываются поэлементно).
Разность двух матриц определяется: А – В = А + (-1)·В.
Умножение матрицы А на матрицу В определяется по формуле: 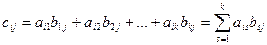 ,
, 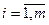 ,
, 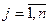 .
.
Матрица 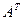 , называется транспонированной относительно матрице А в которой строки и столбцы поменялись местами с сохранением порядка.
, называется транспонированной относительно матрице А в которой строки и столбцы поменялись местами с сохранением порядка.
Определитель матрицы А обозначается 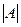 или ∆.
или ∆.
Определителем матрицы второго порядка называется число, которое вычисляется по формуле 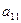
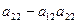 .
.
Аналогично, вводится определитель третьего порядка. Определителем третьего порядка, называется число, которое вычисляется по формуле
∆= 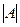 =
= 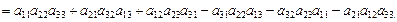
Минором 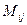 элемента
элемента 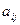 матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-ой строки и j-го столбца.
матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-ой строки и j-го столбца.
Алгебраическим дополнением 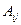 элемента
элемента 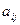 матрицы n-го порядка называется его минор, взятый со знаком
матрицы n-го порядка называется его минор, взятый со знаком 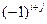 , т.е.
, т.е. 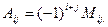
 2015-08-21
2015-08-21 282
282







