Пусть в n –канальной СМО действуют два потока: входной поток заявок и поток освобождений каналов. Пусть оба потока являются простейшими с интенсивностью соответственно λ и μ.
СМО с отказами характерна тем, что если заявка застаёт свободным хотя бы один канал, то она принимается к обслуживанию и обслуживается до конца любым из свободных каналов. Если же заявка застаёт все n каналов занятыми, то она получает отказ и покидает систему необслуженной.
СМО с отказами описывается следующим множеством состояний:
S 0 – все n каналов свободны, в системе нет заявок;
S 1 – занят один канал, обслуживается 1 заявка;
…
S k – занято 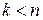 каналов, обслуживается k заявок;
каналов, обслуживается k заявок;
…
S n – заняты все n каналов, обслуживается n заявок.
Граф состояний и переходов для СМО с отказами может быть представлен в следующем виде:
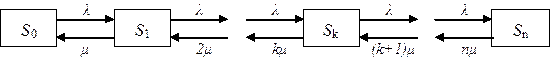
Рисунок 1
Система алгебраических уравнений, описывающая стационарный режим работы СМО и составленная по графу состояний и переходов имеет следующий вид:
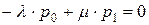
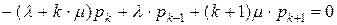 , где
, где 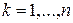
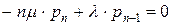
Решениями данной системы являются соотношения, известные как формулы Эрланга:
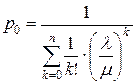
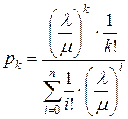 , где
, где 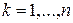
Формулы Эрланга дают предельный закон распределения вероятностей числа занятых каналов в зависимости от параметров входного потока заявок l и потока обслуживания m.
Показатели функционирования СМО:
- вероятность отказа заявке в обслуживании: 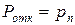 ;
;
- вероятность того, что поступившая заявка будет принята к обслуживанию: 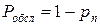 ;
;
- среднее число занятых каналов: 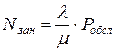 ;
;
- вероятность того, что занят любой канал: 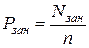 ;
;
- среднее время простоя канала: 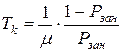 ;
;
- среднее время полной загрузки системы: 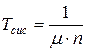 .
.
 2015-08-21
2015-08-21 169
169







