2015-08-21
945
Если в смешанной задаче однородное дифференциальное уравнение и нулевое граничное условие, то её можно решить более коротким, чем в п. 3. способом. Такая задача сводится к задаче Коши, начальные условия которой являются продолжениями на всю ось абсцисс начальных условий исходной смешанной задачи. Для примера рассмотрим такую краевую задачу в области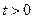 
, 
:
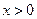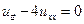(4.1.)
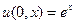(4.2.)
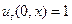(4.3.)
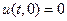(4.4.I)
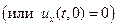(4.4.II)
Если дана смешанная задача с граничным условием (4.4.I), то начальные условия ex и 1, заданные при 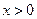, надо продолжить на левую половину 
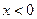оси абсцисс нечётным образом. Если же смешанная задача с граничным условием (4.4.II), то эти функции надо продолжить чётным образом. Напомним, что функция называется нечётной на промежутке (– a; a) (в частности, 
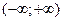), если она отвечает условию f (– x) = – f (x), и называется чётной, если выполняется равенство f (– x) = f (x). График нечётной функции имеет центр симметрии в начале координат. График чётной функции имеет ось симметрии – ось ординат.
Таким образом, решение задачи (4.1.) – (4.4.I) совпадает с решением задачи Коши
, 
, 
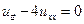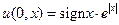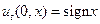, (4.5.)
а решение задачи (4.1.) – (4.3.), (4.4.II) совпадает с решением задачи Коши
, 
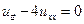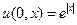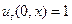, . (4.6.)
Как мы помним, общее решение уравнения 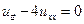есть
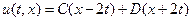. (4.7.)
Решим, например задачу Коши (4.5.). Из её начальных условий и формулы (4.7.) получаем
, 
.
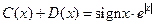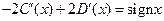Проинтегрируем второе из полученных равенств.
.
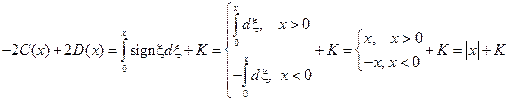Теперь остаётся, как в пункте 1., найти C (x) и D (x) и подставить их в (4.7.).
Упражнение. Закончите решение задачи (4.5.) и решите задачу (4.6.).
