Пусть в области 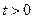 дано уравнение
дано уравнение 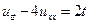 (1.1.)
(1.1.)
с начальными условиями
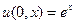 (1.2.)
(1.2.)
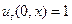 (1.3.)
(1.3.)
Проинтегрируем сначала дифференциальное уравнение (1.1.). Его общее решение есть сумма некоторого его частного решения и общего решения однородного уравнения:
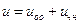 .
.
Разыскивая частное решение в виде функции, зависящей только от t (ибо такова правая часть уравнения!), легко найдём
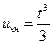 .
.
Стало быть, 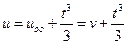 . Теперь функция v находится из уравнения
. Теперь функция v находится из уравнения 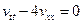 , которое в канонических координатах
, которое в канонических координатах 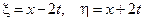 приобретает вид (вспомните прошлое занятие!)
приобретает вид (вспомните прошлое занятие!) 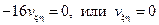 . Отсюда, как мы уже знаем, получается
. Отсюда, как мы уже знаем, получается 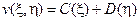 .
.
Возвращаясь к старым переменным, получим 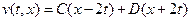 . Значит, общее решение уравнения (1.1.) есть
. Значит, общее решение уравнения (1.1.) есть 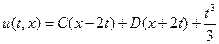 (1.4.)
(1.4.)
Теперь надо найти функции C (x -2 t) и D (x +2 t) из условий (1.2.), (1.3.). Чтобы применить условие (1.3.), продифференцируем решение (1.4.) по t:
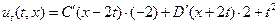 (1.5.).
(1.5.).
Обратите внимание, что в формуле (1.5.) штрихи при буквах C и D означают производные по (x -2 t) и по (x +2 t) соответственно, а не по t.
Полагая в (1.4.) и (1.5.) t = 0, и применяя начальные условия (1.2.) и (1.3.), получим
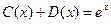 ,
, 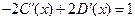 .
.
В последнем равенстве штрихи означают уже производные по x, поскольку оба аргумента (x -2 t) и (x +2 t) при t = 0 обращаются в x. Интегрируя по x последнее равенство, а предпоследнее умножая на 2, получим 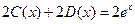 ,
, 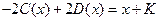 . Отсюда уже легко найти, складывая и вычитая почленно последние равенства, что, соответственно,
. Отсюда уже легко найти, складывая и вычитая почленно последние равенства, что, соответственно, 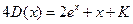 ,
, 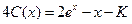 . Теперь в найденных функциях C (x) и D (x) заменим x на (x -2 t) и (x +2 t) соответственно, и подставим функции C (x -2 t) и D (x +2 t) в (1.4.):
. Теперь в найденных функциях C (x) и D (x) заменим x на (x -2 t) и (x +2 t) соответственно, и подставим функции C (x -2 t) и D (x +2 t) в (1.4.):
|
|
|
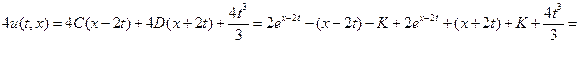
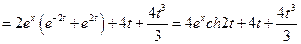 .
.
Следовательно, 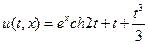 – решение данной задачи Коши.
– решение данной задачи Коши.
Упражнение. Решите задачу Коши в области t > 0:
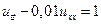 ,
,
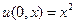 ,
,
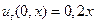 .
.
2. Задача Гурсá.
В области 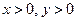 рассмотрим следующую краевую задачу:
рассмотрим следующую краевую задачу:
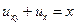 , (2.1.)
, (2.1.)
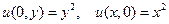 . (2.2.)
. (2.2.)
Уравнение (2.1.) ради экономии времени сразу дано во второй канонической форме. То есть, каноническими переменными здесь являются сами x и y. Заметим, что граничное условие (2.2.), в отличие от задачи Коши, задано на участках x = 0, (при y > 0) и y = 0, (при x > 0) характеристик дифференциального уравнения (2.1.). Задачи с краевыми условиями такого вида называются задачами Гурсá.
Согласно общей схеме метода Даламбера, сначала проинтегрируем уравнение (2.1.). Его правая часть зависит лишь от x. Поэтому в таком же виде найдём и его частное решение 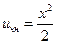 . Соответствующее однородное уравнение
. Соответствующее однородное уравнение 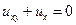 можно решить таким образом:
можно решить таким образом: 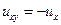 ,
, 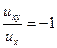 ,
, 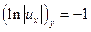 ,
, 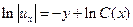 ,
, 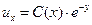 ,
, 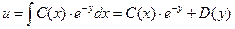 . Следовательно, общее решение есть
. Следовательно, общее решение есть 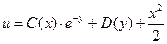 . (2.3.)
. (2.3.)
Теперь, как и при решении задачи Коши, находим пару функций C (x) и D (y) в соответствии с парой условий (2.2.):
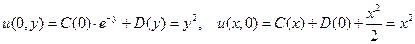 ,
,
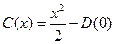
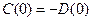
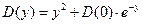 .
.
Найденные функции подставляем в (2.3.): 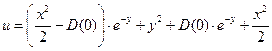 . Таким образом,
. Таким образом, 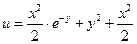 .
.
Упражнение. Решите задачу Гурсá в области y > 0, x > y: 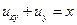 ,
,
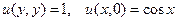 .
.
 2015-08-21
2015-08-21 839
839







