ТРАНСПОРТНАЯ ЗАДАЧА
Важным частным случаем задачи линейного программирования является транспортная задача. Необходимо определить план перевозок некоторого однородного груза, минимизирующий затраты на общую стоимость перевозок, из 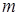 пунктов отправления (производства)
пунктов отправления (производства) 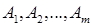 в
в 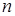 пунктов потребления
пунктов потребления 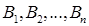 .
.
Введем следующие переменные:
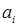 – величина предложения продукта в пункте
– величина предложения продукта в пункте 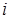 ,
, 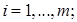
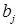 – величина спроса на продукт в пункте
– величина спроса на продукт в пункте 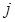 ,
, 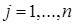 ;
;
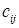 – затраты на транспортировку единицы продукта из пункта
– затраты на транспортировку единицы продукта из пункта 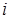 в пункт
в пункт 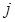 ;
;
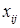 – количество продукта, перевозимого из пункта
– количество продукта, перевозимого из пункта 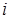 в пункт
в пункт 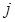 .
.
Тогда транспортную задачу можно представить в виде таблицы 1.
Т а б л и ц а 2.1
| Пункты производства | Пункты потребления | Предложение | |||||
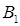
| 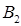
| … | 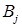
| … | 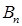
| ||
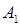
| 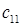
| 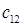
| … | 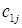
| … | 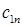
| 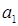
|
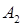
| 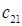
| 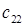
| … | 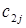
| … | 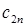
| 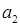
|
| … | … | … | … | … | … | … | … |
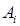
| 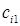
| 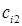
| … | 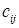
| … | 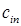
| 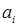
|
| … | … | … | … | … | … | … | … |
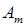
| 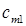
| 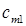
| … | 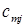
| … | 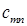
| 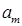
|
| Спрос | 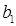
| 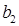
| … | 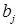
| … | 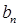
|
В сделанных обозначениях математическую модель транспортной задачи можно записать следующим образом:
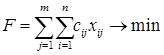 (2.1)
(2.1)
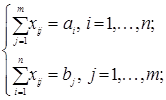 (2.2)
(2.2)
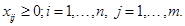 (2.3)
(2.3)
Существует несколько вариантов транспортной задачи.
1. Закрытая транспортная задача
Общий спрос равен общему предложению: 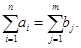
Это равенство является необходимым и достаточным условием существования допустимого плана задачи (2.1) – (2.3).
2. Открытая транспортная задача
а) Пусть существует излишек продукта, т.е. 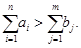
б) Пусть существует дефицит продукта, т.е. 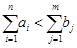
Такую задачу можно свести к закрытой задаче, вводя дополнительный столбец (строку), равный по величине имеющейся разности между общим спросом и общей потребностью, тарифы 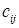 которого считают условно равными нулю.
которого считают условно равными нулю.
3. Транспортная задача с фиксированными перевозками
Если объем перевозок между пунктами 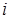 и
и 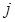 задан, то в задаче (2.1) – (2.3) вводится дополнительное ограничение
задан, то в задаче (2.1) – (2.3) вводится дополнительное ограничение 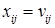 , где
, где 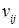 – заданный объем перевозок.
– заданный объем перевозок.
4. Задача с ограничениями на пропускные способности
Если объем перевозок из пункта 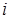 в
в 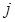 пункт ограничен величиной
пункт ограничен величиной 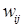 , то в задаче (2.1) – (2.3) вводится дополнительное ограничение
, то в задаче (2.1) – (2.3) вводится дополнительное ограничение 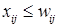 .
.
Все приведенные выше модели описывают транспортную задачу в виде задачи линейного программирования. В этой форме она может быть решена стандартными средствами ЛП, например, с помощью симплекс-метода. Однако специфичная форма системы ограничений данной задачи (в виде уравнений-равенств) позволяет существенно упростить обычный симплекс-метод. Такой метод решения транспортной задачи (ТЗ) называют распределительным, или методом потенциалов. По аналогии с общим случаем ЗЛП, решение в нем осуществляется по трем шагам:
- нахождение первоначального опорного решения;
- проверка критерия оптимальности;
- переход к следующему опорному решению.
 2015-08-21
2015-08-21 314
314








