На трех складах оптовой базы сосредоточен однородный груз в количествах 200, 300 и 500 ед. Этот груз необходимо перевезти в четыре магазина. Каждый из магазинов должен получить соответственно 200, 200, 300 и 400 ед. груза. Тарифы перевозок единицы груза из каждого из складов во все магазины задаются матрицей:
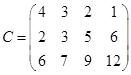
Требуется:
1) составить экономико-математическую модель задачи;
2) найти первоначальное распределение поставок: а) методом северо-западного угла; б) методом минимальных затрат.
3) выбрать лучшее распределение поставок и найти такой план перевозок, при котором общая стоимость перевозок будет минимальной.
Решить транспортную задачу методом потенциалов.
Решение:
1) составление экономико-математической модели ТЗ
Искомый объем перевозки от i -ro поставщика к j -му потребителю обозначим 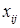 и назовем поставкой клетки
и назовем поставкой клетки 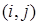 . Заданные объемы груза, имеющегося на базах, и спросы магазинов накладывают ограничения на значения неизвестных. Получаем следующую систему ограничений из уравнений баланса по строкам и столбцам.
. Заданные объемы груза, имеющегося на базах, и спросы магазинов накладывают ограничения на значения неизвестных. Получаем следующую систему ограничений из уравнений баланса по строкам и столбцам.
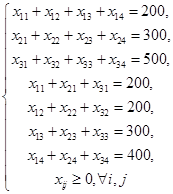
Транспортная задача – задача на минимум. Поэтому целевая функция имеет вид:
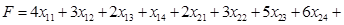
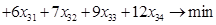
2) найдем первоначальное распределение поставок (опорное решение)
Проверим выполнение необходимого и достаточного условия разрешимости задачи – условие закрытости модели.
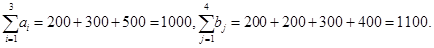
Имеем открытую модель транспортной задачи, необходимо сбалансировать общие итоги. Вводим 4-го, фиктивного поставщика с запасами
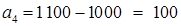
и нулевыми стоимостями перевозок единиц груза.
а) Построим первоначальное распределение поставок методом северо-западного угла:
Распределим запасы первой базы. Так как ее запасы 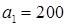 равны потребностям первого магазина
равны потребностям первого магазина 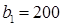 , необходимо ввести условную нулевую поставку, например, по строке. Из дальнейшего рассмотрения исключаются первая строка и первый столбец (см. табл.2.2)
, необходимо ввести условную нулевую поставку, например, по строке. Из дальнейшего рассмотрения исключаются первая строка и первый столбец (см. табл.2.2)
Т а б л и ц а 2.2
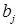 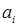 | ||||
 4 4  200 200 | ||||
Распределим запасы второй базы. Так как ее запасы 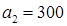 больше потребностей второго магазина
больше потребностей второго магазина 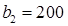 , в клетку
, в клетку 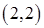 вносим число 200, вычеркиваем второй столбец и запоминаем, что остатки груза на второй базе составляют
вносим число 200, вычеркиваем второй столбец и запоминаем, что остатки груза на второй базе составляют 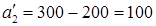 (см. табл.2.3)
(см. табл.2.3)
Т а б л и ц а 2.3
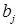 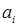 | ||||
 4 4  200 200 |  0 0 | |||
Распределим остатки запасов второй базы. Так как ее запасы 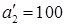 меньше потребностей третьего магазина
меньше потребностей третьего магазина 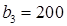 , в клетку
, в клетку 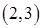 вносим число 100, вычеркиваем вторую строку и запоминаем, что третьему магазину следует допоставить 100 ед. груза (
вносим число 100, вычеркиваем вторую строку и запоминаем, что третьему магазину следует допоставить 100 ед. груза (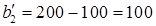 ) (см. табл.2.4)
) (см. табл.2.4)
Т а б л и ц а 2.4
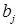 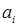 | ||||
 4 4  200 200 | ||||
 3 3  200 200 | ||||
Последовательно выполняя такие действия, получаем первоначальное распределение поставок по методу северо-западного угла, приведенное в таблице 2.5.
Т а б л и ц а 2.5
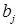 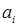 | ||||
Полученное решение 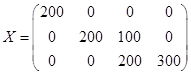 является базисным, т.к. выполняется необходимое и достаточное условие
является базисным, т.к. выполняется необходимое и достаточное условие 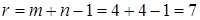 . Найдем значение целевой функции для полученного решения
. Найдем значение целевой функции для полученного решения
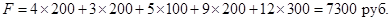
б) Построим первоначальное распределение поставок методом наименьших затрат (минимальной стоимости):
Среди элементов стоимостей выбираем наименьшую стоимость (без учета нулевых стоимостей условной, четвертой базы) 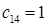 . В соответствующую клетку записываем максимально возможную поставку
. В соответствующую клетку записываем максимально возможную поставку 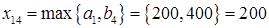 . Потребности 4-го магазина уменьшаем на 400-200=200, вычеркиваем первую строку (табл.2.6).
. Потребности 4-го магазина уменьшаем на 400-200=200, вычеркиваем первую строку (табл.2.6).
Т а б л и ц а 2.6
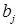 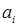 | ||||
 | ||||
В оставшейся части таблицы поставок также определяем элемент с наименьшим тарифом – это 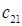 =2. Здесь наибольшая возможная поставка составит
=2. Здесь наибольшая возможная поставка составит 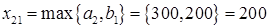 , запасы второй базы уменьшаем до 100 ед., вычеркиваем первый столбец – табл.2.7.
, запасы второй базы уменьшаем до 100 ед., вычеркиваем первый столбец – табл.2.7.
Т а б л и ц а 2.7
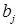 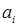 | ||||
 4 4  | ||||
Продолжая таким же образом, получаем первоначальное распределение поставок методом минимальной стоимости, приведенное в таблице 2.8.
Т а б л и ц а 2.8
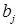 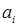 | ||||
Полученное решение имеет 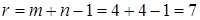 базисных переменных. Вычислим значение целевой функции на этом опорном решении
базисных переменных. Вычислим значение целевой функции на этом опорном решении 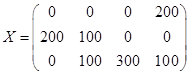 .
.
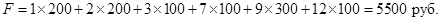
Сравнивая значения целевых функций для опорных планов, полученных методами северо-западного угла и минимальной стоимости, делаем вывод, что целевая функция для второго случая ближе к минимуму.
3) проверка критерия оптимальности найденного решения
По признаку оптимальности в каждой занятой опорным решением таблицы ТЗ сумма потенциалов равна стоимости (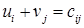 при
при 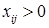 ). Составим систему уравнений для нахождения потенциалов строк и столбцов матрицы поставок
). Составим систему уравнений для нахождения потенциалов строк и столбцов матрицы поставок
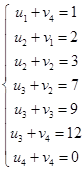
Система состоит из семи уравнений и имеет восемь переменных. Система неопределенная. Одной переменной задаем произвольное значение (пусть 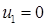 ). Остальные значения потенциалов находятся однозначно:
). Остальные значения потенциалов находятся однозначно:
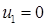 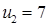 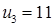 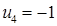 | 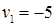 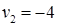 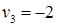 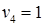 |
Вычислим оценки свободных клеток с учетом найденных потенциалов:
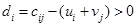
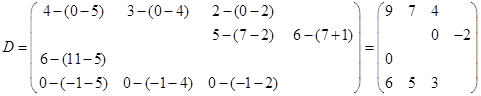
Критерий оптимальности не выполняется, т.к. 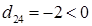 .
.
- переход к следующему опорному решению
Для перехода к следующему базисному решению построим цикл для клетки (2,4) – загрузим ее поставкой (см. табл. 2.9).
Т а б л и ц а 2.9
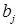 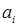 | ||||
 3 3  100 100 |  6 6 | |||
 7 7 |  12 12 | |||
Определим поставку, передаваемую по циклу 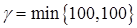 (как наименьшее из чисел, находящихся в вершинах цикла со знаком «-»). Клетку (3,4) с тарифом
(как наименьшее из чисел, находящихся в вершинах цикла со знаком «-»). Клетку (3,4) с тарифом 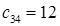 будем считать свободной. Следующее базисное распределение представлено в таблице 2.10
будем считать свободной. Следующее базисное распределение представлено в таблице 2.10
Т а б л и ц а 2.10
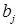 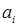 | ||||
Проверим найденное решение на оптимальность. Составим систему уравнений для нахождения потенциалов строк и столбцов новой матрицы поставок
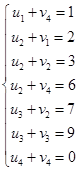
Пусть 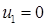 , тогда
, тогда
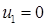 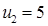 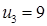 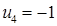 | 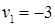 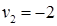 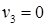 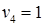 |
Вычислим оценки свободных клеток с учетом найденных потенциалов и проверим выполнение критерия оптимальности:
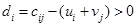
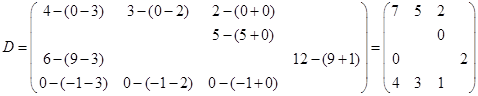
Критерий оптимальности выполняется, следовательно, найденное опорное решение оптимально. Найдем минимальное значение стоимости перевозок:
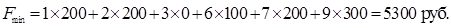
Ответ: 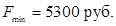 при
при 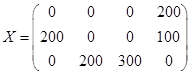 .
.
Контрольные вопросы
1. Как формулируется транспортная задача?
2. В чем состоят особенности транспортной задачи как задачи линейного программирования?
3. Как составляется первоначальное распределение поставок методом северо-западного угла?
4. Как составляется первоначальное распределение поставок методом минимальных затрат?
5. Как решаются транспортные задачи с нарушенным балансом между спросом и предложением?
Тест
1. Транспортная задача будет закрытой, если…
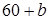 | |||
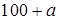 | |||
Варианты ответов:
1) 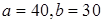 ; 2)
; 2) 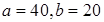 ; 3)
; 3) 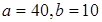 ; 4)
; 4) 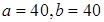 .
.
2. Транспортная задача будет закрытой, если…
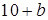 | |||
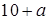 | |||
Варианты ответов:
1) 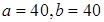 ; 2)
; 2) 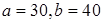 ; 3)
; 3) 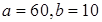 ; 4)
; 4) 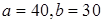 .
.
3. В опорном плане транспортной задачи должно быть следующее количество заполненных клеток:
Варианты ответов:
1) 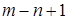 ; 2)
; 2) 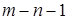 ; 3)
; 3) 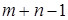 ; 4)
; 4) 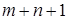 .
.
4. Среди приведенных транспортных задач закрытыми будут являться….
1)
2)
3)
4)
5. Среди приведенных транспортных задач открытыми будут являться….
1)
2)
3)
4)
6. Для транспортной задачи, представленной в таблице
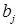  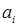 | |||
Начальным опорным планом задачи может быть следующий…
Варианты ответов:
1) 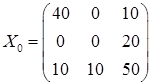 ; 2)
; 2) 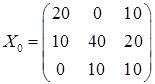 ; 3)
; 3) 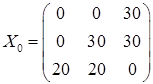 ;
;
4) 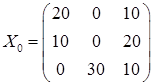
7. Для данного распределения поставок значение целевой функции будет равно…
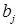 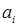 | |||
Варианты ответов:
1)1000; 2) 1200; 3) 6200; 4) 6000.
 2015-08-21
2015-08-21 1001
1001








