Задание 2

Величины 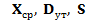случайные и являются точечными оценками математического ожидания М|Х| дисперсии D|X| и среднеквадратического

отклонения 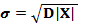наблюдаемой в выборке случайной величины X.

2.1. Предполагая, что наблюдаемая величина X имеет нормальное распределение, построим доверительные интервалы для математического ожидания а=М|Х] и среднеквадратического отклонения 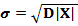при уровне

надежности 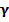=0,99.

Поскольку известно, что величина 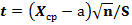имеет распределение Стьюдента с n-1 степенью свободы, то решая уравнение Р(| t |< 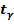,)= 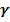относительно 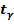можно построить симметричный интервал 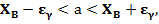в котором с вероятностью 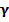находится математическое ожидание а. Величина 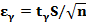представляет собой точность оценки. Решение 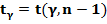есть обращенное распределение Стьюдента, оно протабулировано и может быть найдено и таблиц.

В рассматриваемом примере 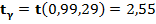, 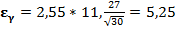и тогда доверительный интервал для математического ожидания будет

35,42-5,25 < а < 35,42+5,25 или 30,17 < а < 40,67.

Для нахождения доверительного интервала оценки среднеквадратнческого отклонения 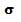воспользуемся тем, что величина 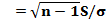имеет распределение «Хи» с n-1 степенью свободы. Задавшись надежностью интервальной оценки 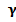и решая уравнение 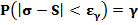относительно 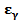можно построить доверительный интервал. Переходя к эквивалентному уравнению 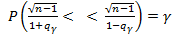, где 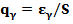, найдем его решение 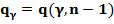из таблиц, тогда точность оценки 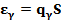. Доверительный интервал строится таким образом: .

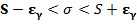В нашем примере 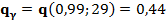тогда 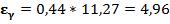и доверительный интервал будет следующий

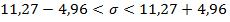или .

В нем оцениваемый параметр находится с вероятностью 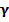=0,99

2.2. Отметим, что построенные доверительные интервалы являются областями принятия гипотез 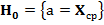и при их проверке с уровнем значимости 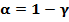. Теперь проверим гипотезу о равенстве математического ожидания и дисперсии наблюдаемой случайной величины указанным в задании гипотетическим значениям , .

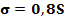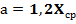Проверяем сначала гипотезу о том, что истинная дисперсия наблюдаемой величины равна 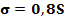, т.е. 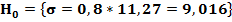. Зададимся уровнем значимости гипотезы 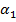=0,05, и альтернативными гипотезам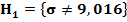и или 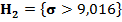. Для проверки основной гипотезы воспользуемся критерием «Хи-квадрат» .

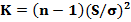Наблюдаемое значение критерия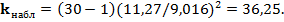

Критическая область 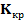при альтернативной гипотезе 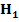двухсторонняя, а критические точки найдем из таблиц 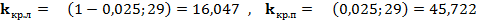. Видим, что 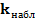не принадлежит критической, области и значит, гипотеза принимается, т.е. отличие наблюдаемого, значения дисперсии от гипотетического не значительны. Если в качестве

альтернативной рассматривать гипотезу Н₂, поскольку 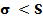значительно (20%), то при этом критическая область будет правосторонней, а критическую точку 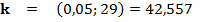найдем -из таблиц. Тогда наблюдаемое значение критерия не попадает в критическую область и проверяемая гипотеза принимается. Результат проверки гипотезы при различных альтернативах оказался разным, в итоге гипотеза принимается.

Проверим теперь гипотезу о том, что истинное математическое ожидание наблюдаемой величины равна 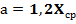, т.е. 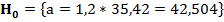. Зададимся уровнем значимости гипотезы 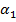=0,05 и альтернативными гипотезами 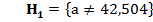или Для проверки основной гипотезы воспользуемся критерием Стьюдента .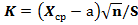

Наблюдаемое значение критерия 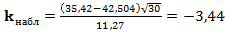. Критическая область 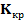при альтернативной гипотезе 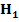двухсторонняя, а критические точки найдем из таблиц 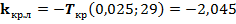, 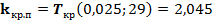. Видим, что 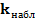принадлежит критической области и значит, гипотеза отвергается, т.е. отличие наблюдаемого значения дисперсии от гипотетического значительны. Если в качестве альтернативной рассматривать гипотезу Н₂, поскольку 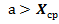значительно (20%), то критическая область левосторонняя, а критическая точка 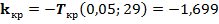, тогда наблюдаемое значение 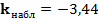попадает в критическую областьпроверяемая гипотеза опять отвергается. Результат проверки гипотезы при различных альтернативах оказался одинаковым, в итоге гипотеза отвергается.

2.3. Проверим гипотезу об однородности выборки, т.е. гипотезу о равенстве математического ожидания и дисперсии случайных величин, наблюдаемых в первой и второй половинах имеющейся выборки.

Разобьем выборку на две равные части объемов 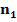=15, 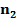=15 и вычислим

по ним выборочные средние и выборочные стандарты

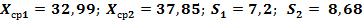
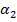Основная проверяемая гипотеза . Зададимся уровнем значимости гипотезы =0,05 и альтернативными гипотезам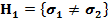и или 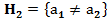, поскольку отличия в значениях 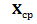, 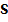для разных частей выборки не существенны (менее чем 16%)_.

Для проверки основной гипотезы по отношению к альтернативной гипотезе 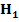воспользуемся критерием Фишера

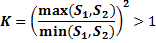
Наблюдаемое значение критерия 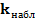=1,453. Критическая область 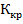при альтернативной гипотезе 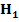правосторонняя, а критическую точку найдем из таблиц 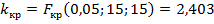. Видим, что 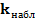не принадлежит критической области и значит, гипотеза принимается. Если в качестве альтернативной рассматривать гипотезу Н₂, то для проверки основной гипотезы воспользуемся критерием Стьюдента

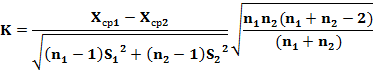
Наблюдаемое значение критерия 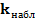= -1,669. Критическая область 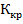при этом 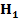двухсторонняя, а критические точки найдем из таблиц 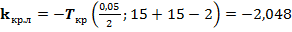, 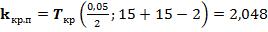. Видим, что 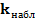не принадлежит критической области и значит, гипотеза опять принимается, т.е. отличие наблюдаемых значений математического ожидания и дисперсии в первой и второй половине выборки незначительны. Гипотеза об однородности выборки принимается.