Задание 3

3.1. Построим гистограмму выборки 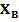как удобную форму представления выборочного распределения. Для этого разобьём наблюдаемый интервал значений в выборке на m равновеликих интервалов

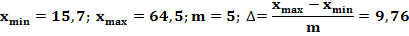
Количество интервалов разбиения m выбирается исходя из свойств

выборки, рекомендуется., использовать формулу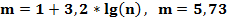

примем m=5. Граничные точки интервалов 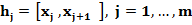иих

центры вычисляем по формулам следующим образом:

Подсчитав для каждого интервала частоты попадания в него элементов

выборки 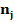и относительные частота 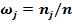, сведем все результаты расчета

наблюдаемых частот 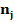, 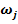в следующую таблицу 2 и построим гистограмму

частот рис. 2.

Таблица 2

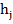
	15,7-25,46	25,46-35,22	35,22-44,98	44,98-54,74	54,74-64,5	Σ
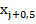
	20,58	30,34	40,10	49,86	59,62
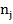
	6,00	9,00	11,00	2,00	2,00	30,00
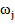
	0,200	0,300	0,367	0,067	0,067	1,000
Теоретические частоты нормальной случайной величины
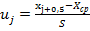
	-1,316770	-0,450754	0,415262	1,281278	2,147294
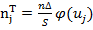
	4,364640	9,352800	9,508680	4,572480	1,034004	28,832604
	0,612743	0,013308	0,233895	1,447279	0,902461	3,209686
Теоретические частоты показательной случайной величины
	4,608	3,506	2,667	2,030	1,544	14,355
	0,421	8,610	26,028	0,000	0,134	35,195

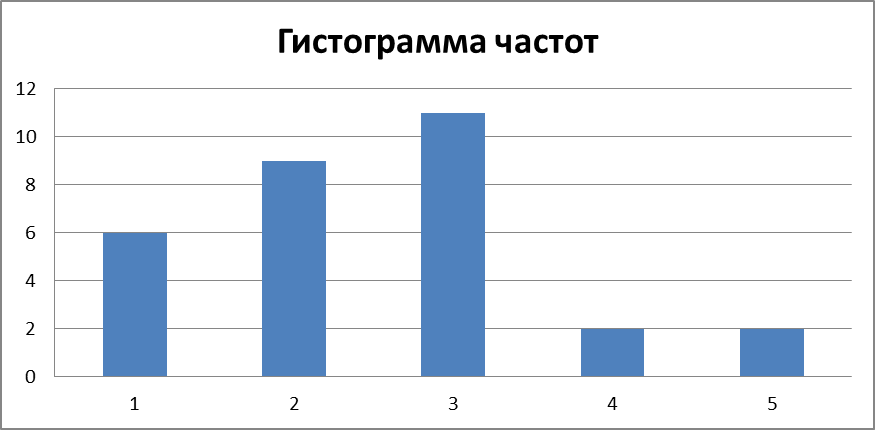
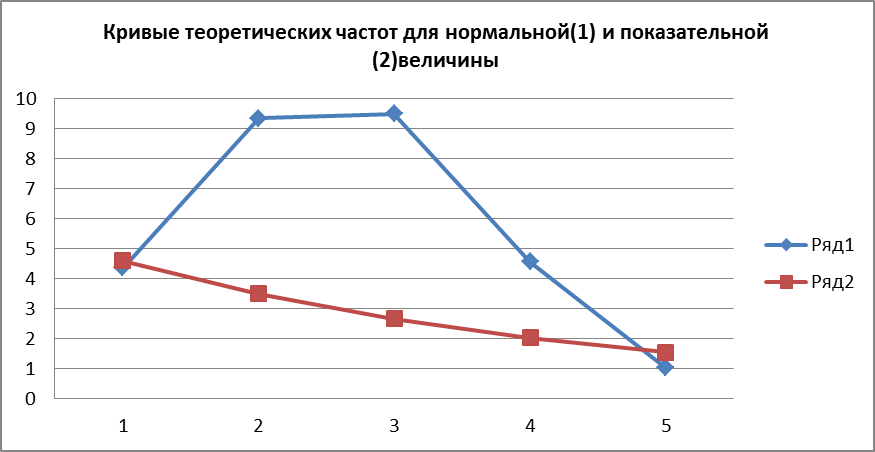
Рис. 2

3.2. Используя критерий согласия Пирсона, проверим гипотезу 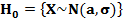о нормальном распределении наблюдаемой случайной величины X с параметрами a = 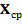, 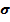=S. Для этого подсчитаем теоретические частоты попадания величины X в интервалы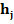

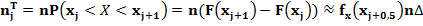
Поскольку проверяется гипотеза о нормальном распределении то

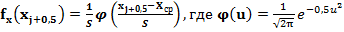- функция Гаусса.

Все результаты расчетов теоретических частот 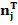приведены в таблице 2 и на рис. 2, где приводится так же кривая теоретических частот.

Согласно критерия Пирсона величина суммарного отклонения наблюдаемых частот от теоретических

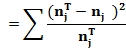
при условии справедливости основной гипотезы имеет распределение «хи-квадрат» с m-З степенями свободы и может быть принята за критерий проверки гипотезы 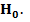Задаваясь уровнем значимости ошибки II-рода (отвергнуть верную гипотезу) 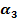=0,01 находим критическую точку критерия из решения уравнения

Его решения представляются обратным «хи-квадрат» распределением и находятся из таблиц. Тогда критерий проверки основной гипотезы 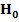о нормальном распределении выборочного признака X состоит в следующем:

если гипотеза принимается (отклонения

теоретических и наблюдаемых частот не значительны),

если гипотеза отвергается (отклонения значительны)

В нашем примере величина рассчитана в таблице и ее значение,а. Тогда согласно критерию Пирсона гипотеза о нормальном распределении случайной величины X принимается.

3.3. Теперь проверим гипотезу Но ={Х ~Е()} о показательном распределении наблюдаемой случайной величины X с параметром =1/Хс_Р. Теоретические частоты подсчитаем исходя из вида фикции плотности показательного распределения

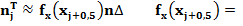
Рассчитанные теоретические частоты; и суммарное относительное отклонение наблюдаемых и теоретических частот приводятся так же в таблице 2 и отражены на рис. 2.

Из таблицы видно, что наблюдаемое значение критерия при проверке гипотезы =35,195 принадлежит правосторонней критической области, так как критическая точка (0,01;5-2)= 11,3. Тогда согласно критерию Пирсона гипотеза о показательном распределении наблюдаемой случайной величины X отклоняется.