У даній механічній системі (див. схеми у звіті до лабораторної роботи) колеса 1 і 2 механізму обертаються навколо нерухомих осей, а вантаж 3 здійснює поступальний рух.
Запишемо диференціальні рівняння руху кожного з цих трьох тіл, для чого відділимо одне від одного, розрізавши нитку, що утримує вантаж 3, і роз´єднаємо колеса 1 і 2 у точках стикування зубців (див. розрахункову схему).
До колеса 1 прикладена сила ваги m1 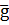 , рушійний момент М, складові реакції підшипника
, рушійний момент М, складові реакції підшипника 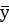 А,
А, 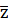 А, окружне зусилля
А, окружне зусилля 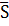 1 і нормальна реакція
1 і нормальна реакція 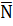 1 колеса 2.
1 колеса 2.
До колеса 2 механізму прикладені сила ваги m2 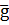 , момент сил опору Мс, складові реакції підшипника
, момент сил опору Мс, складові реакції підшипника 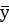 b,
b, 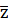 b, сила натягнення
b, сила натягнення 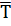 нитки, до якої причеплений вантаж 3, окружне зусилля
нитки, до якої причеплений вантаж 3, окружне зусилля 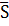 2 і нормальна реакція
2 і нормальна реакція 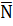 2 колеса 1.
2 колеса 1.
До вантажа 3 прикладені сила ваги m3 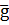 і натягнення нитки
і натягнення нитки 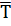 1.
1.
Очевидно, що
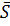 2 = −
2 = − 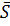 1,
1, 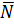 1 = −
1 = − 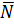 2,
2, 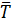 1 = −
1 = − 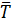 .
.
Диференціальне рівняння обертального руху колеса 1 навколо осі х1 складаємо у вигляді
Iх1 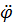 1 =
1 = 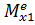 ,
,
де 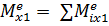 – головний момент зовнішніх сил, прикладених до колеса 1, відносно осі обертання х1:
– головний момент зовнішніх сил, прикладених до колеса 1, відносно осі обертання х1:
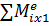 = Μ – S1R1.
= Μ – S1R1.
(Момент М приводить до руху колесо 1 і тому прийнятий додатним, а момент, що здійснюється окружним зусиллям 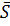 1, перешкоджає обертанню колеса 1 і, таким чином, від´ємний).
1, перешкоджає обертанню колеса 1 і, таким чином, від´ємний).
Диференціальне рівняння обертального руху колеса 1 приймає вигляд:
 1 = Μ – S1R1. (1)
1 = Μ – S1R1. (1)
Складемо диференціальне рівняння обертального руху колеса 2 навколо осі х2:
Iх2 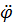 2 = ∑
2 = ∑ 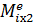
або
Iх2 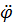 2 = S2R2 − T
2 = S2R2 − T 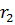 −
− 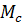 . (2)
. (2)
(Знаки моментів сил 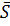 2,
2, 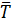 і моменту сил опору
і моменту сил опору 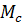 прийняті за тим же правилом, що і при складанні рівняння (1)).
прийняті за тим же правилом, що і при складанні рівняння (1)).
Складемо диференціальне рівняння поступального руху вантажа 3:
m3 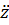 = ∑F
= ∑F 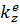 ,
,
де проекція головного вектора зовнішніх сил, прикладених до вантажа 3, на вісь z, спрямовану у бік руху вантажа, тобто догори:
∑F 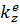 = T1 – m3g
= T1 – m3g
І, таким чином, маємо диференціальне рів неня у вигляді
m3 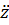 = T1 – m3g.
= T1 – m3g.
В рівняннях (1), (2), (3) невідомими є сили T1 = T, S1 = S2 = S, а також функції 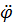 1(t),
1(t), 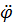 2(t) і
2(t) і 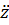 (t) – кутові прискорення колес 1, 2 і прискорення вантажа 3відповідно. Але зазначені функції пов´язані між собою співвідношеннями
(t) – кутові прискорення колес 1, 2 і прискорення вантажа 3відповідно. Але зазначені функції пов´язані між собою співвідношеннями
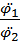 =
= 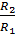 , (4)
, (4)
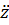 =
= 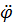 2r2. (5)
2r2. (5)
Таким чином, із врахуванням (4) і (5) система рівнянь (1), (2), (3) може бути зведена до системи з трьома невідомими T, S і 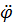 2, тобто розв´язується цілком алгебраїчно.
2, тобто розв´язується цілком алгебраїчно.
Числове вирішення наведено у прикладі звіту лабораторної роботи.
Визначити рівняння руху тіла системи, вказаного в останньому стовбчику таблиці вихідних даних.
Визначити також …
 2015-08-12
2015-08-12 304
304








