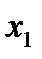Записать исходную ФАЛ во всех случаях заданий по п. №1,2,3 в базисах Вебба и Шеффера; минимизировать её методами неопределенных коэффициентов, минимизирующих карт, Квайна, Квайна-Мак-Класки, карт Карно. Сравнить результаты.
Запишем исходную ФАЛ во всех случаях заданий п. №1,2,3 в базисе Вебба:
Решение:
Функция трех переменных:
| Таблица 1 | ||||||||
| x 1 | ||||||||
| x 2 | ||||||||
| x 3 | ||||||||
| f(x 1, x 2, x 3) |
Используя алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы в базисе n-местной функции Вебба, получим:
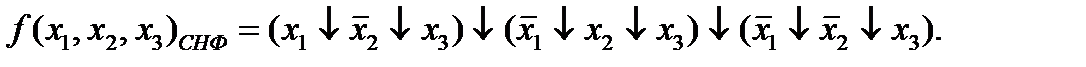
Функция четырех переменных:
| Таблица 2 | ||||||||||||||||
| x 1 | ||||||||||||||||
| x 2 | ||||||||||||||||
| x 3 | ||||||||||||||||
| x 4 | ||||||||||||||||
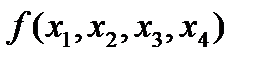
|
Используя алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы в базисе n-местной функции Вебба, получим:
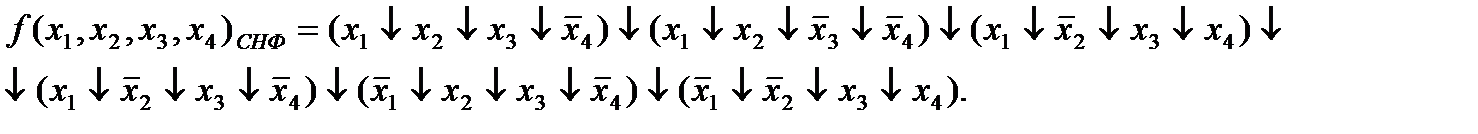
Функция пяти переменных:
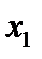
| 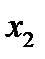
| 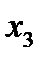
| 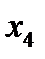
| 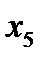
| 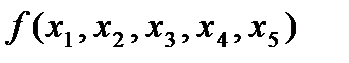
|
Используя алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы в базисе n-местной функции Вебба, получим:
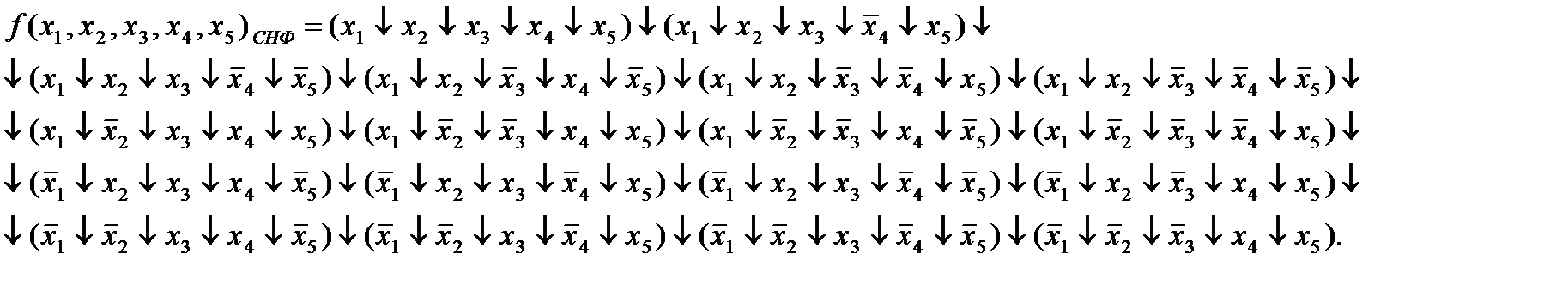
Запишем исходную ФАЛ во всех случаях заданий п. №1,2,3 в базисе Шеффера:
Решение:
Функция трех переменных:
| Таблица 1 | ||||||||
| x 1 | ||||||||
| x 2 | ||||||||
| x 3 | ||||||||
| f(x 1, x 2, x 3) |
Используя алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы в базисе n-местной функции Шеффера, получим:
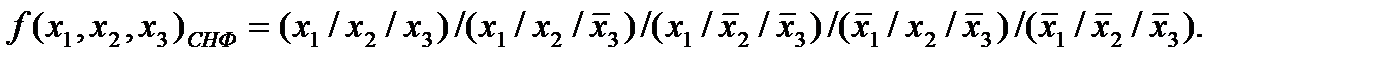
Функция четырех переменных:
| Таблица 2 | ||||||||||||||||
| x 1 | ||||||||||||||||
| x 2 | ||||||||||||||||
| x 3 | ||||||||||||||||
| x 4 | ||||||||||||||||
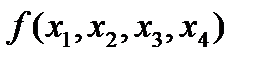
|
Используя алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы в базисе n-местной функции Шеффера, получим:
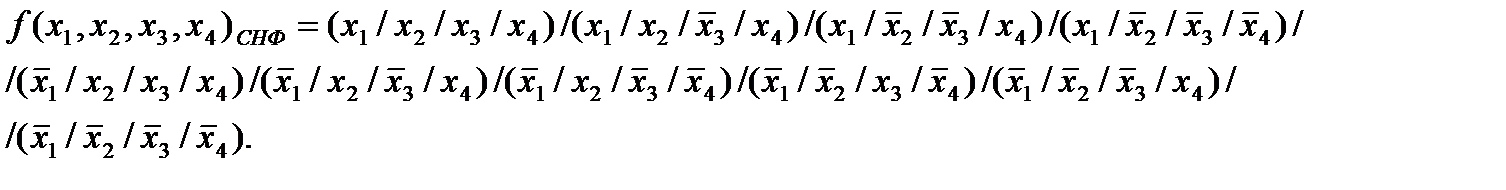
Функция пяти переменных:
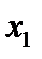
| 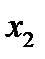
| 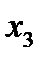
| 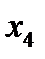
| 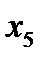
| 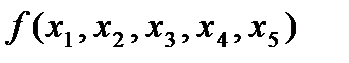
|
Используя алгоритм перехода от табличного задания функции к ее записи в виде совершенной нормальной формы в базисе n-местной функции Шеффера, получим:
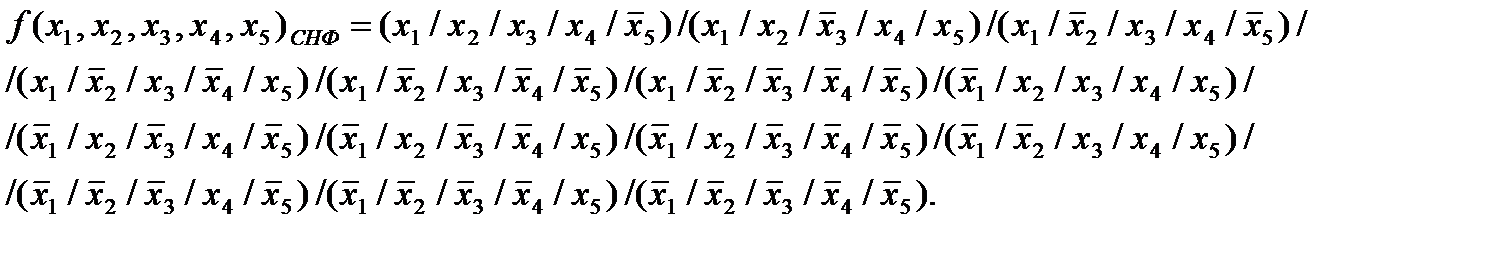
Преобразования и минимизация в базисе, состоящем из функции Вебба:
Решение:
Функция трех переменных: 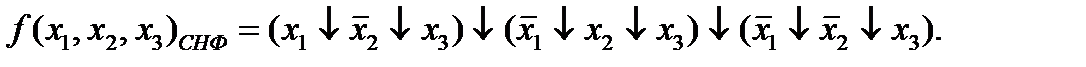
Метод неопределенных коэффициентов:
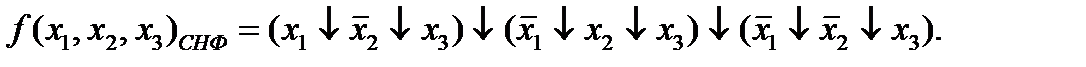
Переходя к системе уравнений с неопределенными коэффициентами для данной функции, получаем:
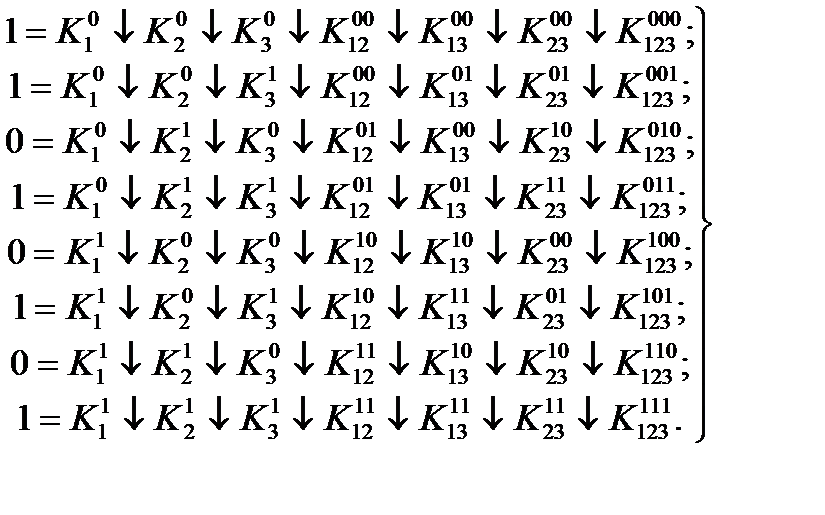
С учетом того, что все коэффициенты для уравнений, у которых в левой части стоит единица, равны нулю, преобразуем исходную систему к следующему виду:
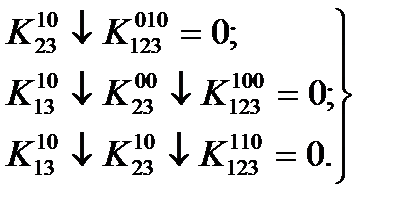
Приравняем к единице коэффициент 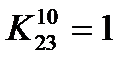 . Наиболее экономное решение для двух оставшихся уравнений
. Наиболее экономное решение для двух оставшихся уравнений  ,
, 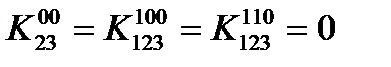 .
.
Окончательно: 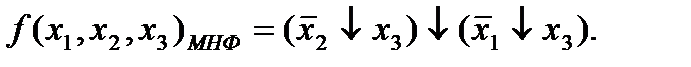
Ответ: 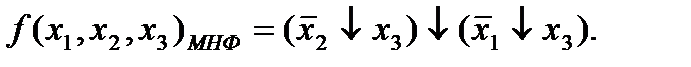
Метод минимизирующих карт:
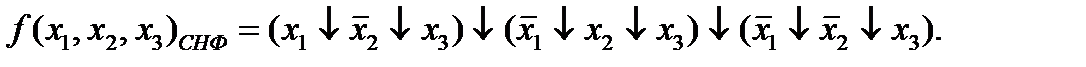
Строим для функции минимизирующую карту:
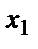
| 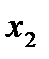
| 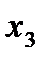
| 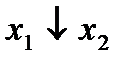
| 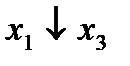
| 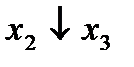
| 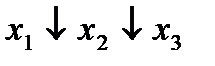
|
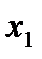
| 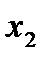
| 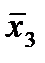
| 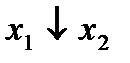
| 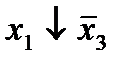
| 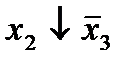
| 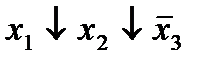
|
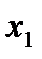
| 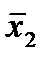
| 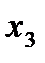
| 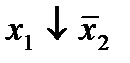
| 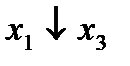
| 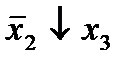
| 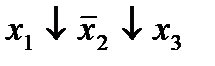
|
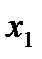
| 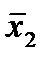
| 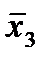
| 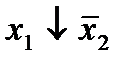
| 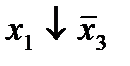
| 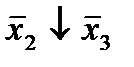
| 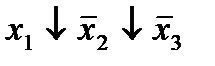
|
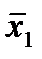
| 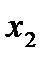
| 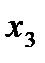
| 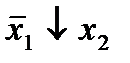
| 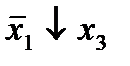
| 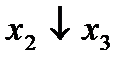
| 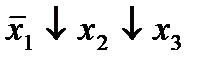
|
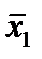
| 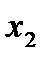
| 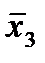
| 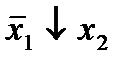
| 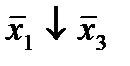
| 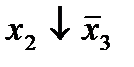
| 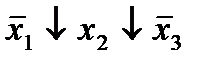
|
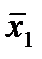
| 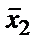
| 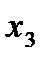
| 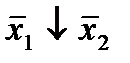
| 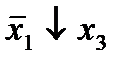
| 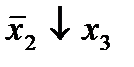
| 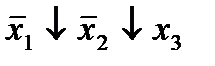
|
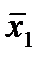
| 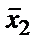
| 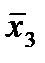
| 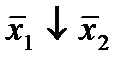
| 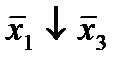
| 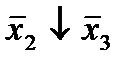
| 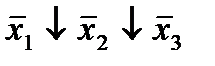
|
Отметим в последнем столбце те конъюнкции, которые входят в СНФ данной функции. Вычеркнем неотмеченные строки, затем вычеркнем в остальных строках (действуя по столбцу) те элементы, которые попали в вычеркнутые строки. В 6-ом столбце (с двумя переменными) положим 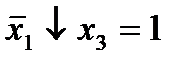 , при этом остальные элементы строк 5, 7, где стоит элемент
, при этом остальные элементы строк 5, 7, где стоит элемент 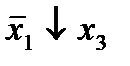 , положим равными нулю. В столбце 6 положим элемент
, положим равными нулю. В столбце 6 положим элемент 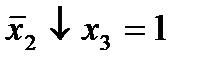 , следовательно, получим МНФ данной функции в виде:
, следовательно, получим МНФ данной функции в виде: 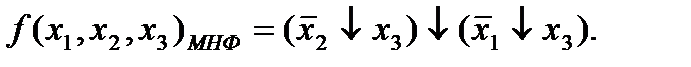
Ответ: 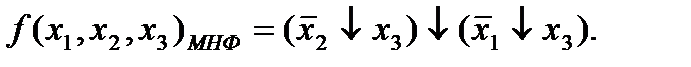
Метод Квайна:
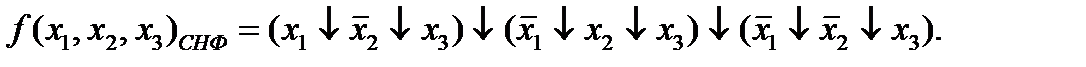
Для удобства вычисление построим таблицу и сделаем в ней преобразования, опирась на ранее изложенный алгоритм:
Члены 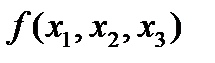
| Результат 1-го склеивания | |
| 1. | 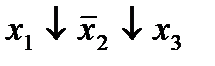 * *
| 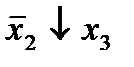 (1,3) (1,3)
|
| 2. | 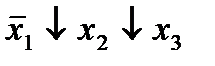 * *
| 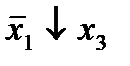 (2,3) (2,3)
|
| 3. | 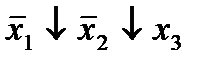 * *
|
Исходя из результатов очевидна МНФ данной функции: 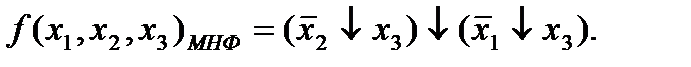
Ответ: 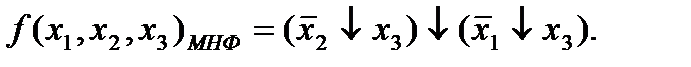
Метод Квайна-Мак-Класки:
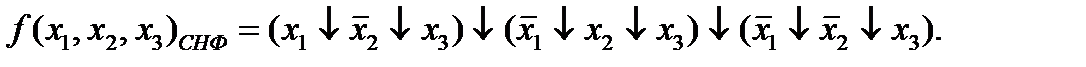
Заменим исходные импликанты их кодами в двоичных переменных:
010, 100, 110.
Разобьем коды исходных импликант на группы, поместим их в таблицу. Далее применим закон склеивания к членам соседних групп, перебирая каждый член 1-й группы со всеми членами 2-й группы и т.д.
Все преобразования сделаем сразу в таблице:
| Группа | Ранг | |
| 010 * | -10 | |
| 100 * | 1-0 | |
| 110 * |
После обработки таблицы получаем окончательный ответ:
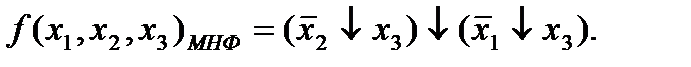
Ответ: 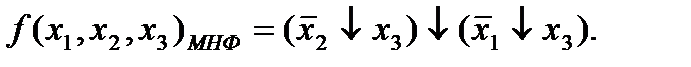
Метод карт Карно:
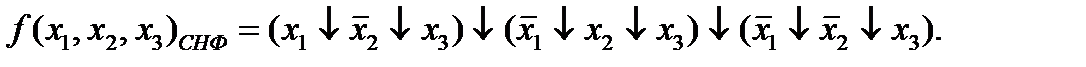
|
|
|
Ответ: 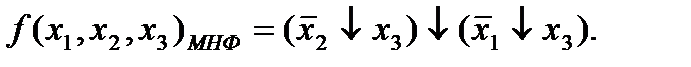
Функция четырех переменных:
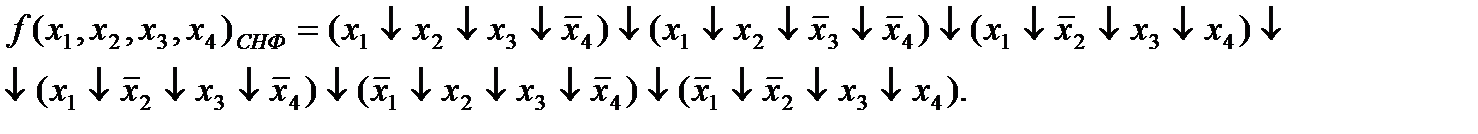
Метод неопределенных коэффициентов:
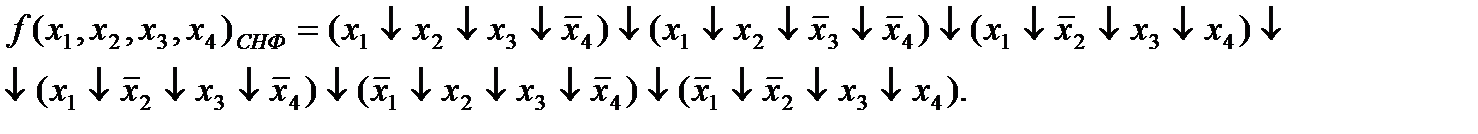
Опираясь на вышеизложенные алгоритмы, составим систему уравнений с неопределенными коэффициентами для данной функции, получаем:
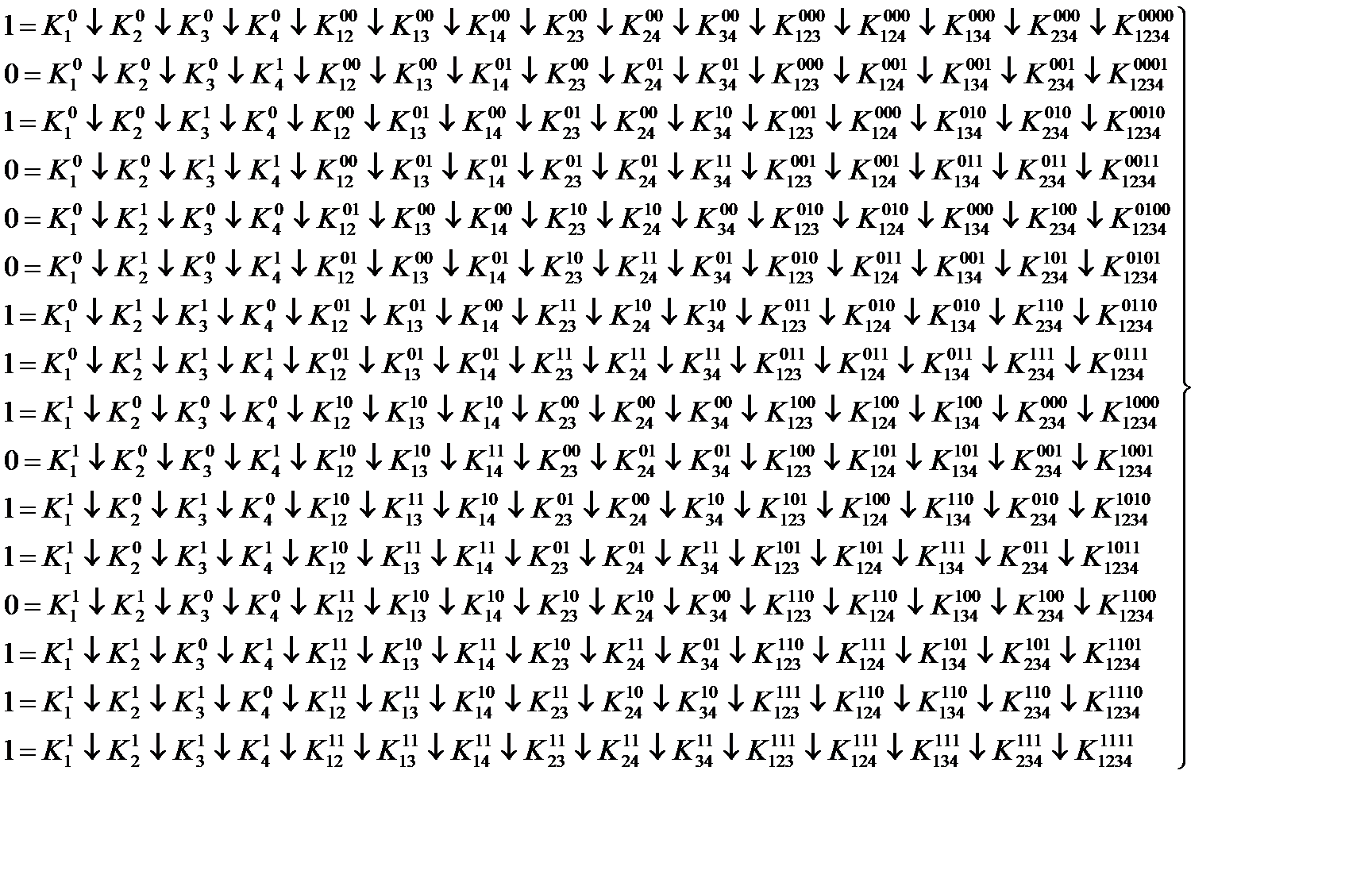
С учетом того, что все коэффициенты для уравнений, у которых в левой части стоит единица, равны нулю, преобразуем исходную систему к следующему виду:

Приравняем к единице коэффициент 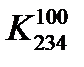 =1. Наиболее экономное решение для четырех оставшихся уравнений:
=1. Наиболее экономное решение для четырех оставшихся уравнений:
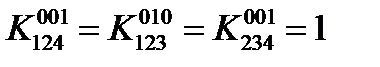 ,
, 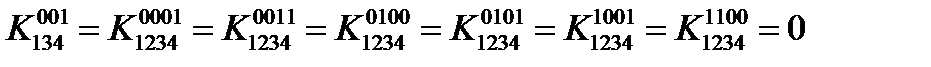 .
.
Окончательно: 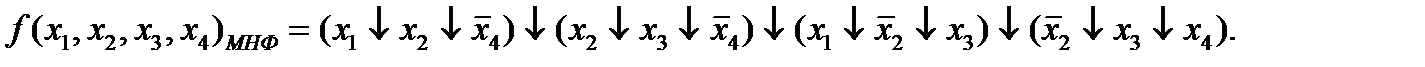
Ответ: 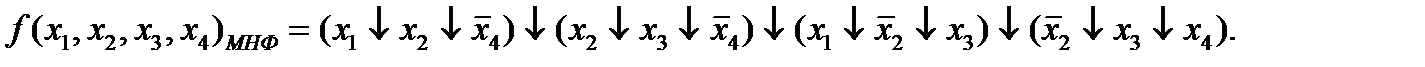
Метод минимизирующих карт:
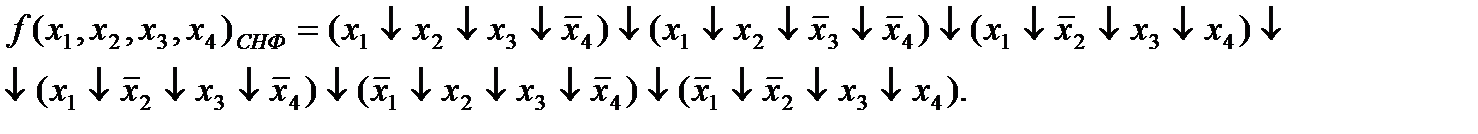
Построим для данной функции минимизирующую карту:
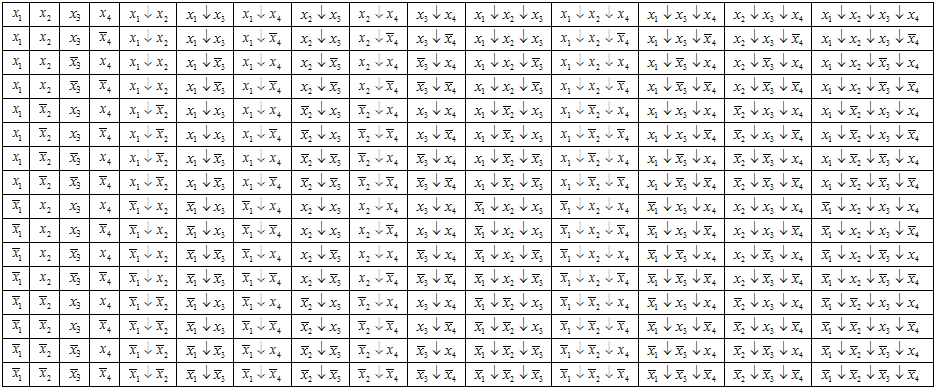
Работа с картой производится аналогично классическому методу. Обведем прямоугольником те элементы, которые остались после вычеркивания.
Пусть 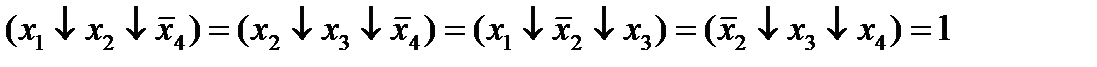 , тогда все остальные элементы будут равны нулю.
, тогда все остальные элементы будут равны нулю.
В результате этих преобразований получаем окончательный ответ:
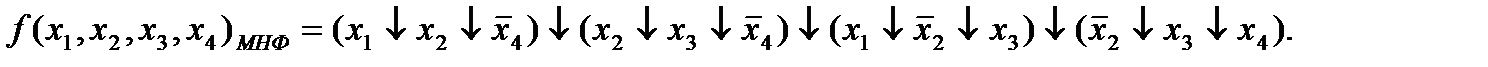
Ответ: 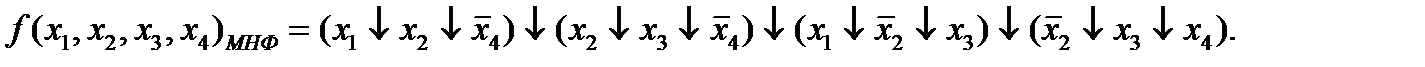
Метод Квайна:
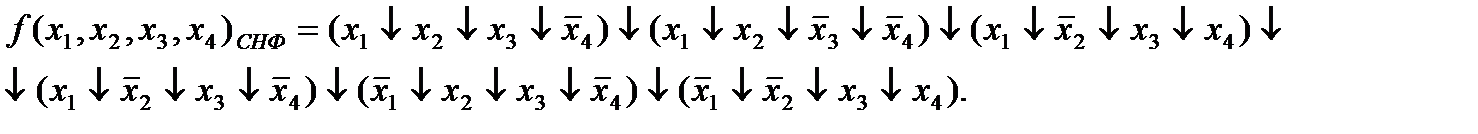
С помощью таблицы получим минитермы 3-го и 2-го рангов:
Члены 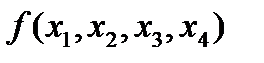
| Результат 1-го склеивания | |
| 1. | 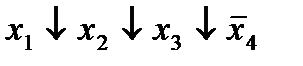 * *
| 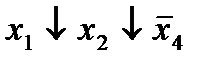 (1,2) (1,2)
|
| 2. | 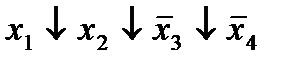 * *
| 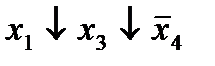 (1,4) (1,4)
|
| 3. | 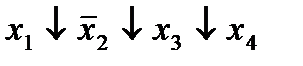 * *
| 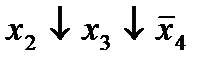 (1,5) (1,5)
|
| 4. | 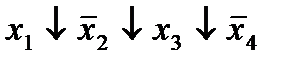 * *
| 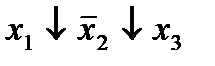 (3,4) (3,4)
|
| 5. | 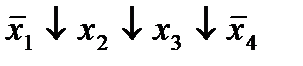 * *
| 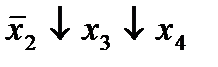 (3,6) (3,6)
|
| 6. | 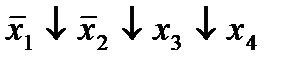 * *
|
Строим таблицу меток (см. приложение №1, стр.47).
Как известно, по методу Квайна получаются тупиковые формы. Обработка таблицы в данном случае подтверждает это утверждение. Найдем минимальное покрытие. Выбирается такая совокупность первичных импликант, которая бы имела метки во всех столбцах. Предпочтение отдается варианту покрытия с минимальным числом букв в первичных импликантах, образующих покрытие. Учитывая все указания, запишем тупиковую форму данной функции, которая одновременно является и минимальной формой:
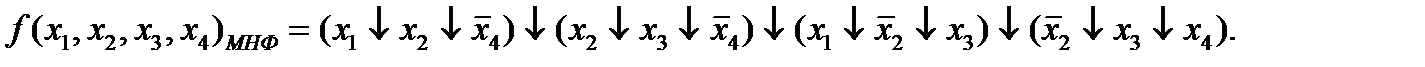
Ответ: 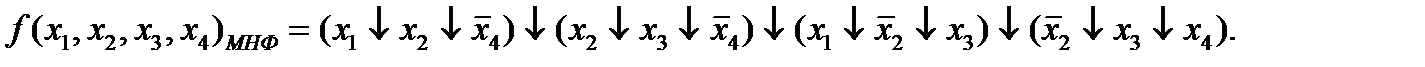
Метод Квайна-Мак-Класки:
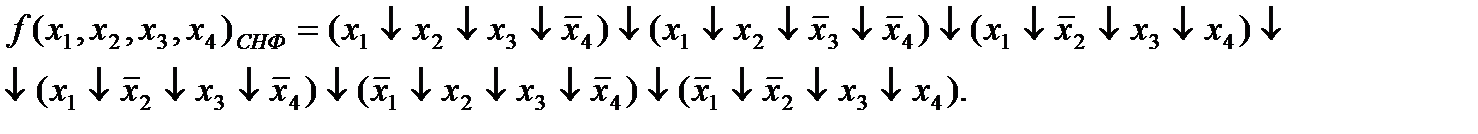
Заменим исходные импликанты их кодами в двоичных переменных:
0001, 0011, 0100, 0101, 1001, 1100.
Разобьем коды на группы, поместим их в таблицу. Далее применим закон склеивания к членам соседних групп, перебирая каждый член 1-й группы со всеми членами 2-й группы и т.д.
Все преобразования сделаем сразу в таблице:
| Данная функция | Результаты 1-го склеивания | ||||
| Коды | Группы | Коды | Группы | ||
| 1-я | 0001 * | 00-1 | 1-я | -001 | |
| 0100 * | 0-01 | -100 | |||
| 2-я | 0011 * | -001 | 2-я | 0-01 | |
| 0101 * | 010- | 3-я | 00-1 | ||
| 1001 * | -100 | 4-я | 010- | ||
| 1100 * |
Строим таблицу меток:
| -001 | v | v | ||||
| -100 | v | v | ||||
| 0-01 | v | v | ||||
| 00-1 | v | v | ||||
| 010- | v | v |
Обработка производится аналогично предыдущему методу (Квайна).
В результате мы получаем:
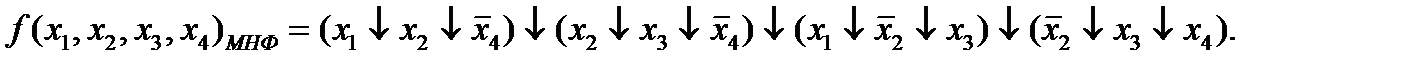
Ответ: 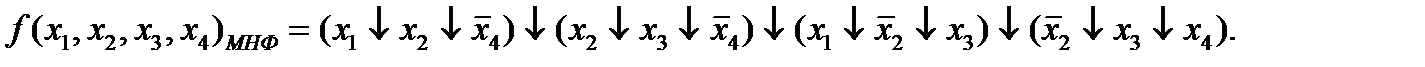
Метод карт Карно:
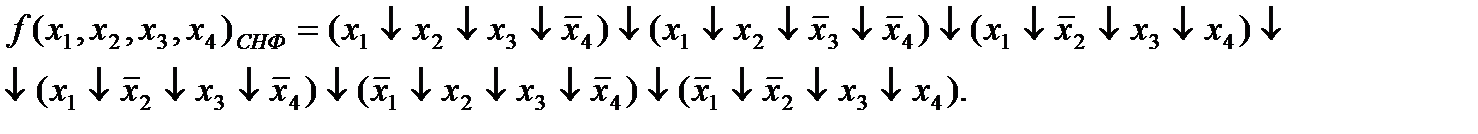
Строим карту Карно:
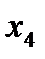
|
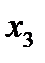
|
| ||||
| ||||
Ответ: 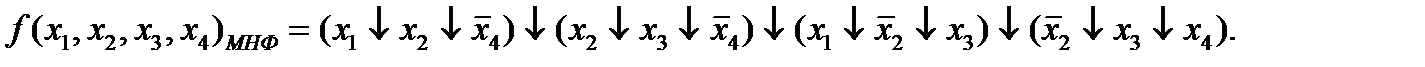
Функция пяти переменных:
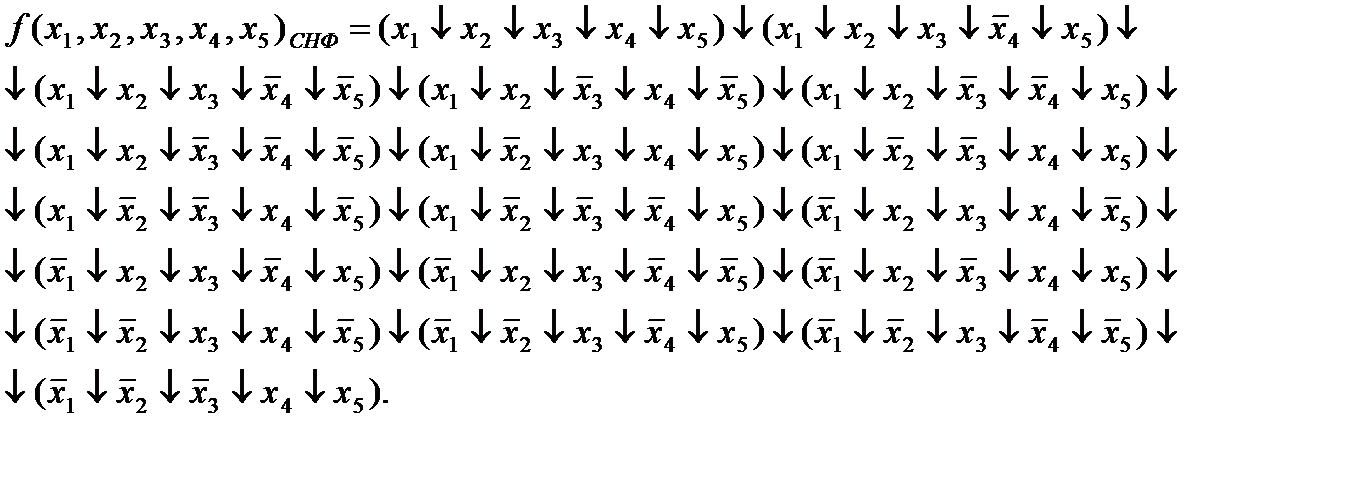
Метод неопределенных коэффициентов:
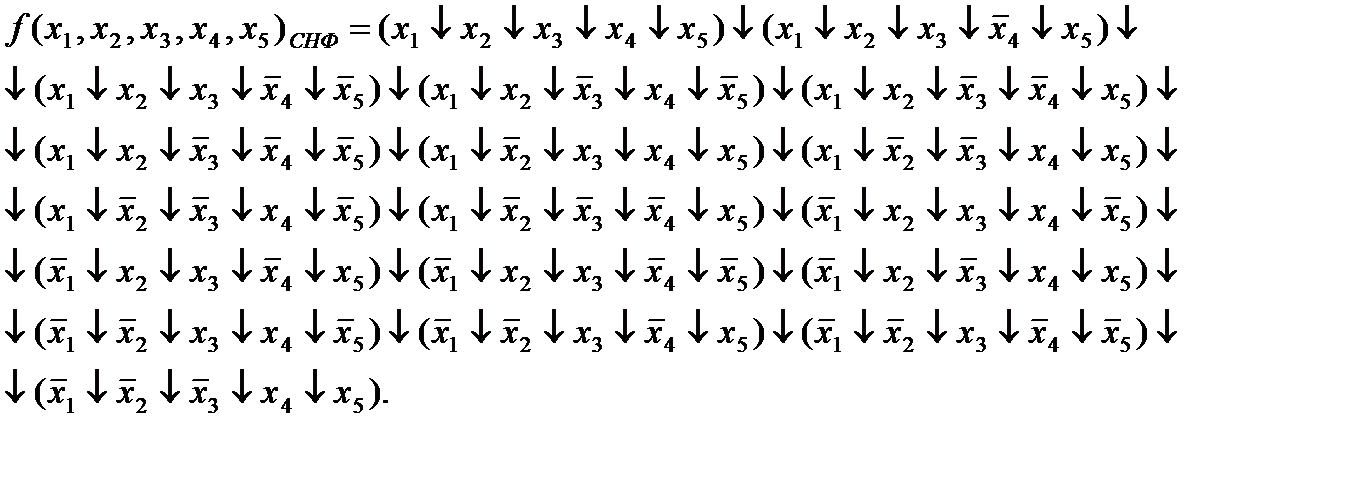
Опираясь на вышеизложенные алгоритмы, составим систему уравнений с неопределенными коэффициентами для данной функции (см. Приложение №2, стр.48).
С учетом того, что все коэффициенты для уравнений, у которых в левой части стоит единица, равны нулю, преобразуем исходную систему к следующему виду: (см.след.стр.)
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Из полученной системы следует, что 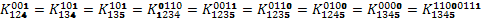 . Значит, все остальные элементы будут
. Значит, все остальные элементы будут
равны 0.
В результате этих преобразований получаем:
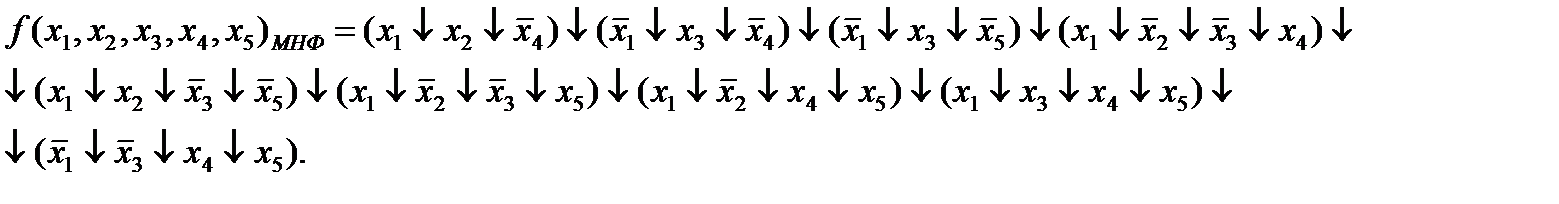
Ответ:
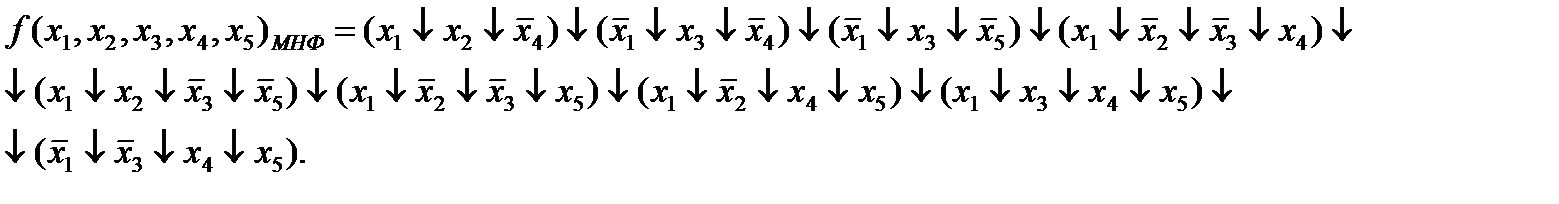
Метод минимизирующих карт:
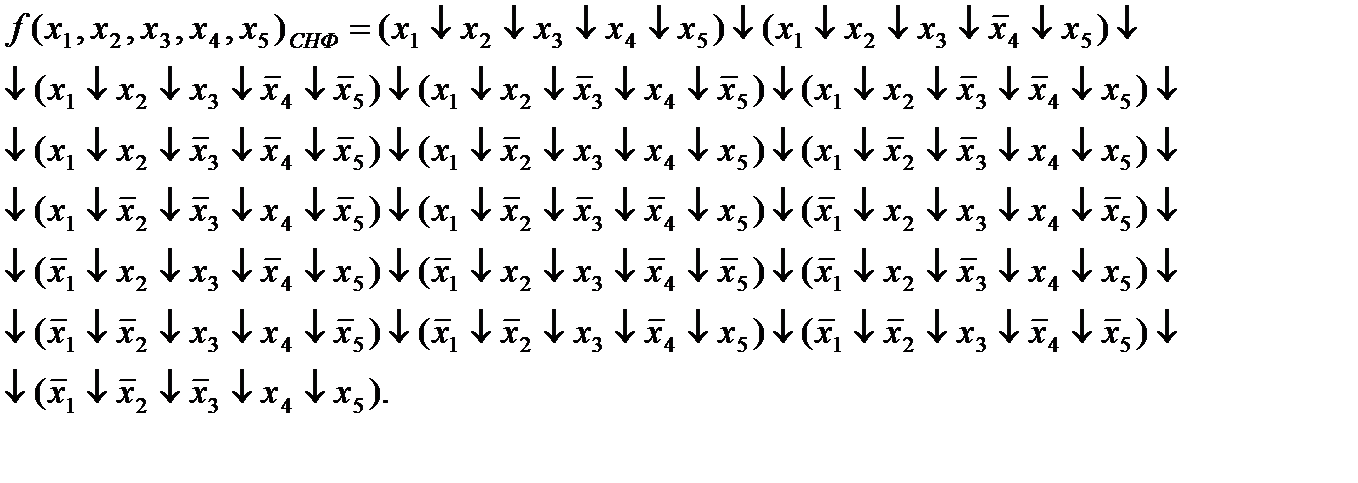
Построим для данной функции минимизирующую карту в базисе Вебба и обработаем ее аналогично классическому методу. (см. Приложение №3, стр.49).
Работа с картой производится аналогично классическому методу (обведем те элементы, которые не вычеркиваются в ходе работы).
Оставшиеся элементы будут равны 0.
Ответ:
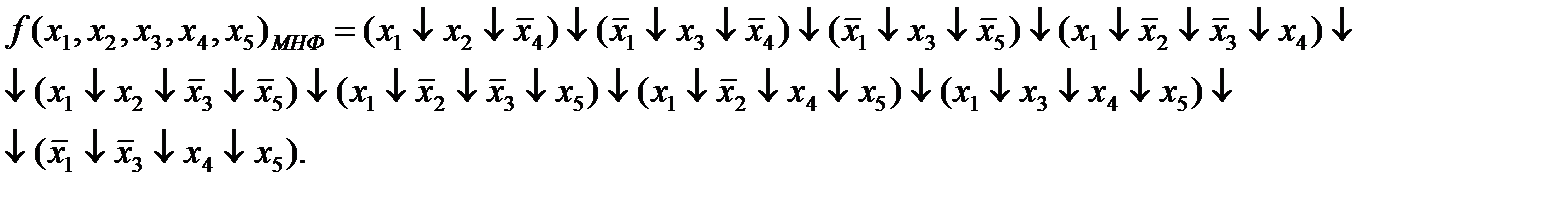
Метод Квайна:
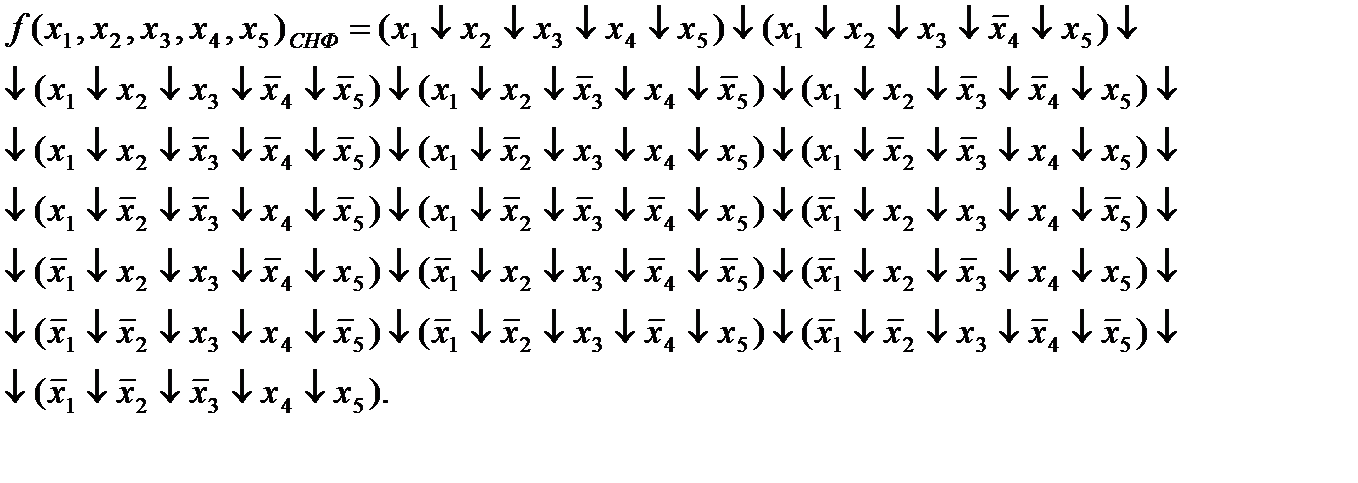
С помощью таблицы получим минитермы 3-го и 2-го рангов:
Члены 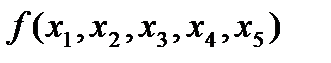
| Результат 1-го склеивания | Результат 2-го склеивания | |
| 1. | 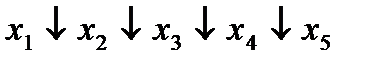 * *
| 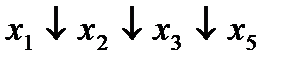 (1,2) (1,2)
| 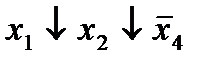 (3,10) (3,10)
|
| 2. | 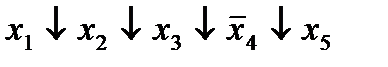 * *
| 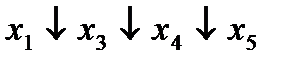 (1,7) (1,7)
| 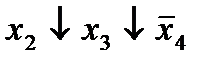 (3,18) (3,18)
|
| 3. | 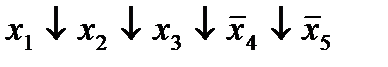 * *
| 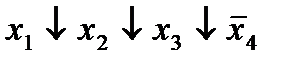 (2,3)* (2,3)*
| 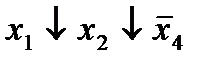 (4,6) (4,6)
|
| 4. | 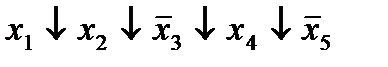 * *
| 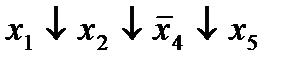 (2,5)* (2,5)*
| 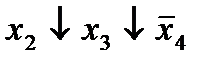 (5,7) (5,7)
|
| 5. | 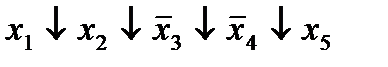 * *
| 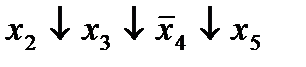 (2,12)* (2,12)*
| 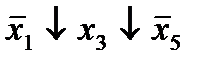 (16,22) (16,22)
|
| 6. | 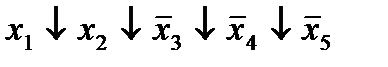 * *
| 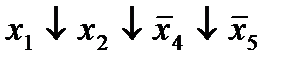 (3,6)* (3,6)*
| 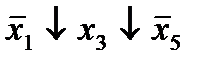 (17,20) (17,20)
|
| 7. | 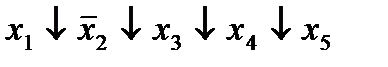 * *
| 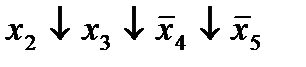 (3,13)* (3,13)*
| 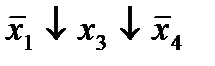 (18,23) (18,23)
|
| 8. | 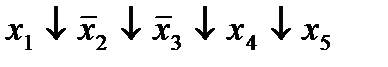 * *
| 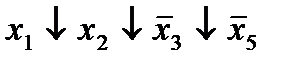 (4,6) (4,6)
| |
| 9. | 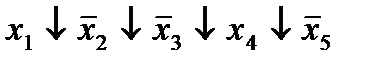 * *
| 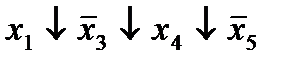 (4,9) (4,9)
| |
| 10. | 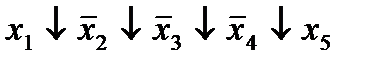 * *
| 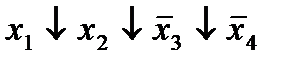 (5,6)* (5,6)*
| |
| 11. | 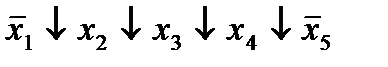 * *
| 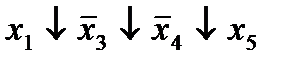 (5,10) (5,10)
| |
| 12. | 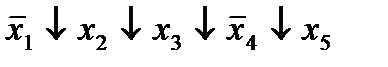 * *
| 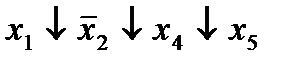 (7,8) (7,8)
| |
| 13. | 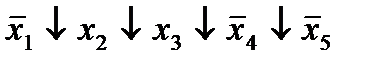 * *
| 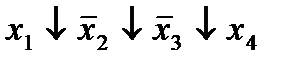 (8,9) (8,9)
| |
| 14. | 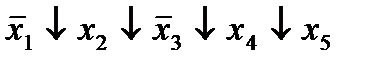 * *
| 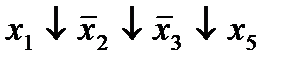 (8,10) (8,10)
| |
| 15. | 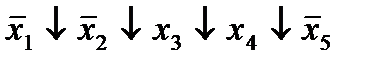 * *
| 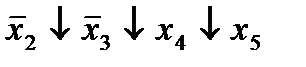 (8,18) (8,18)
| |
| 16. | 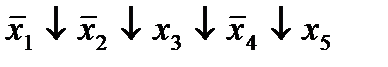 * *
| 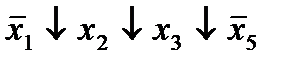 (11,13)* (11,13)*
| |
| 17. | 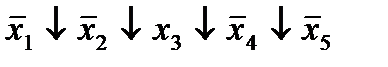 * *
| 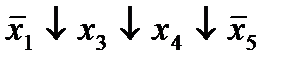 (11,15)* (11,15)*
| |
| 18. | 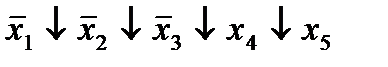 * *
| 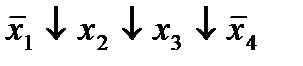 (12,13)* (12,13)*
| |
| 19. | 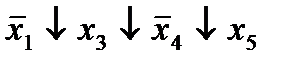 (12,16) (12,16)
| ||
| 20. | 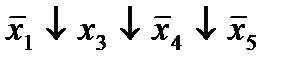 (13,17)* (13,17)*
| ||
| 21. | 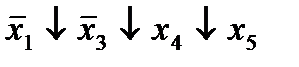 (14,18) (14,18)
| ||
| 22. | 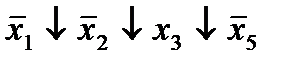 (15,17)* (15,17)*
| ||
| 23. | 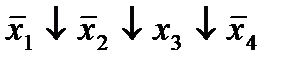 (16,17) (16,17)
|
Построим таблицу меток (см. Приложение №4, стр.50).
Ответ:
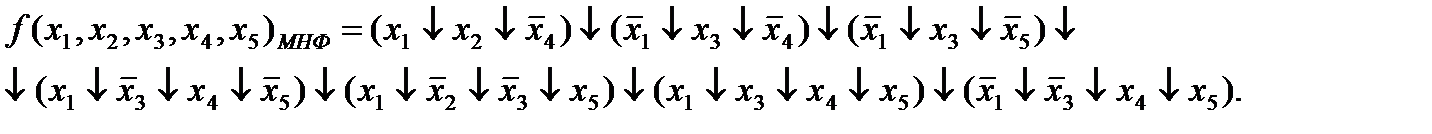
Метод Квайна-Мак-Класки:
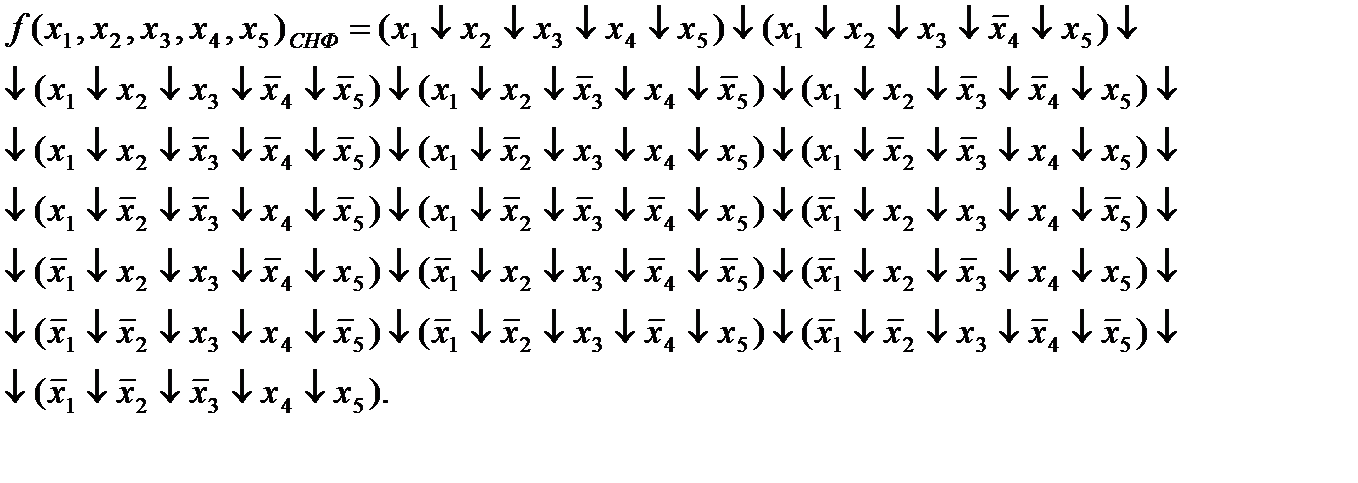
Заменим исходные импликанты их кодами в двоичных переменных:
00000, 00010, 00011, 00101, 00110, 00111, 01000, 01100, 01101, 01110, 10001, 10010, 10011, 10100, 11001, 11010, 11011, 11100.
Разобьем коды исходных импликант на группы, поместим их в таблицу. Далее применим закон склеивания к членам соседних групп, перебирая каждый член 1-й группы со всеми членами 2-й группы и т.д.
Все преобразования сделаем сразу в таблице (см. след. стр.).
| Группа | Ранг | ||
| 0-я | 00000* | 000-0 | 00-1- |
| 1-я | 00010* | 0-000 | -001- |
| 01000* | 0001-* | 00-1- | |
| 2-я | 00011* | 00-10* | -001- |
| 00101* | -0010* | 1-0-1 | |
| 00110* | 01-00 | 1-0-1 | |
| 01100* | 00-11* | 1-01- | |
| 10001* | -0011* | ||
| 10010* | 001-1 | ||
| 10100* | 0-101 | ||
| 3-я | 00111* | 0011-* | |
| 01101* | 0-110 | ||
| 01110* | 0110- | ||
| 10011* | 011-0 | ||
| 11001* | -1100 | ||
| 11010* | 100-1* | ||
| 11100* | 1-001* | ||
| 4-я | 11011* | 1001-* | |
| 1-010* | |||
| 1-100 | |||
| 1-011* | |||
| 110-1* | |||
| 1101- |
Далее построим таблицу меток, в нее впишем исходные и первичные импликанты в виде двоичных кодов(см. приложение №5, стр.51):
После обработки таблицы, получаем тупиковые формы. Дальнейшая работа с таблицей аналогична методу Квайна.
Ответ:
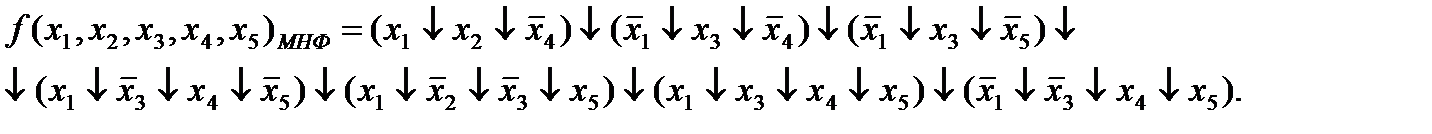
Метод карт Карно:
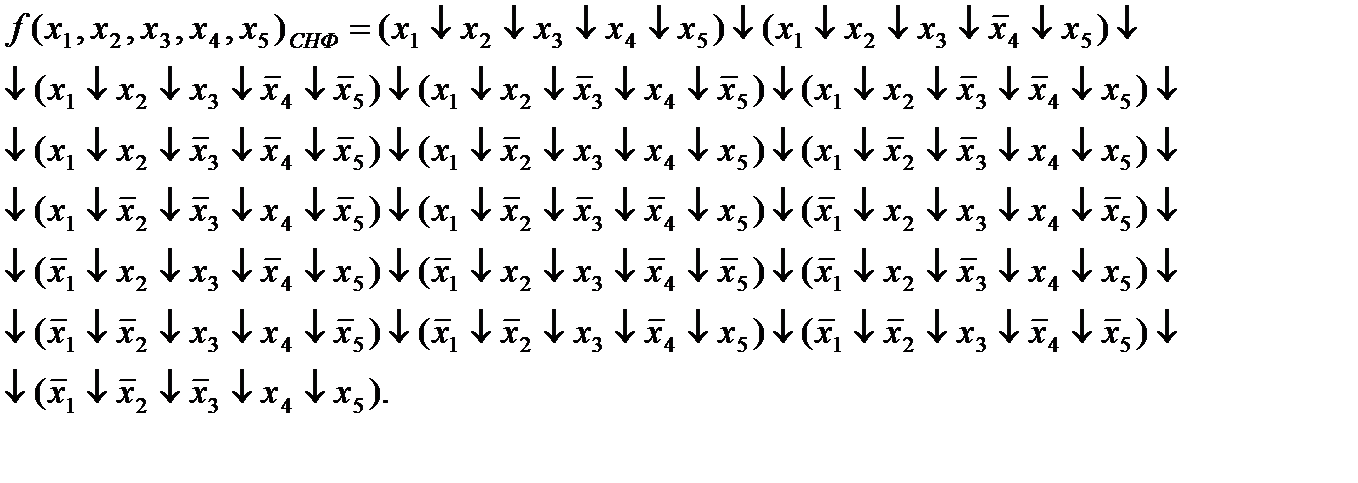
Построим карту Карно:
|
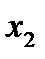
|
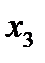
|
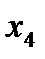
|
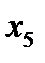
|
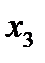
|
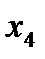
|
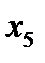
|
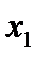
|
|
Ответ:
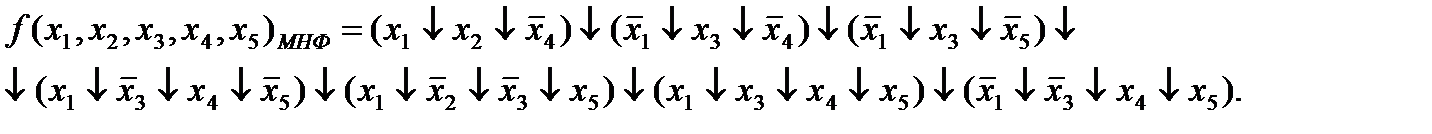
Преобразования и минимизация в базисе, состоящем из функции Шеффера:
Решение:
Функция трех переменных:
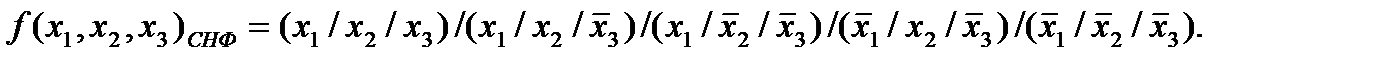
Метод неопределенных коэффициентов:
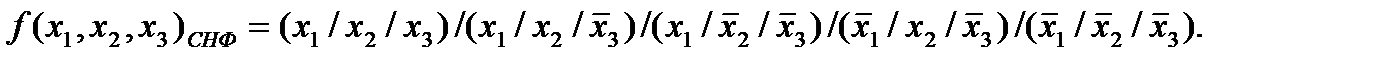

Вычеркнем уравнения, в левой части которых стоят нули, а в остальных уравнениях вычеркнем коэффициенты равные нулю. После этих преобразований система примет вид:
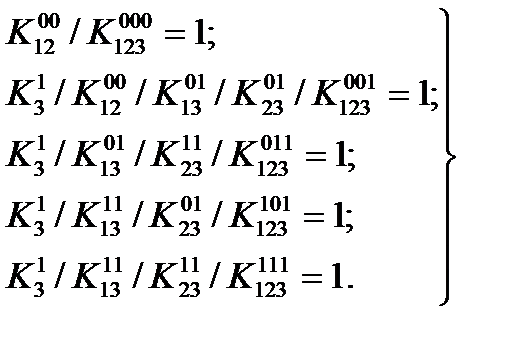
Приравняем к единице коэффициент 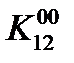 =1. Наиболее экономное решение для четырех оставшихся уравнений
=1. Наиболее экономное решение для четырех оставшихся уравнений 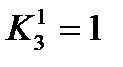 ,
, 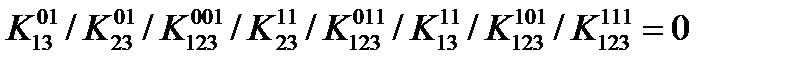 .
.
Окончательно: 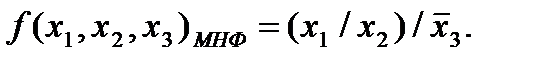
Ответ: 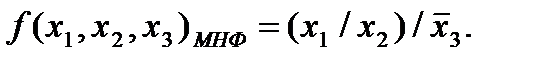
Метод минимизирующих карт:
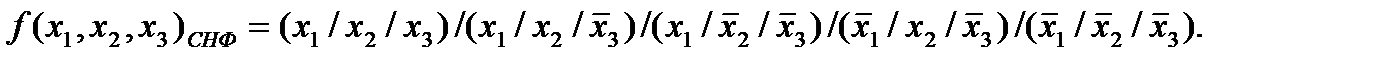
Строим для функции минимизирующую карту:
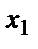
| 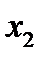
| 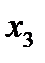
| 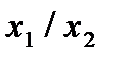
| 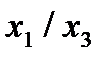
| 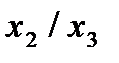
| 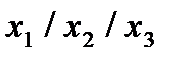
|
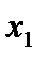
| 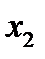
| 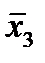
| 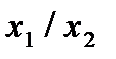
| 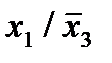
| 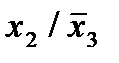
| 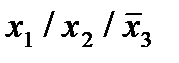
|
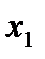
| 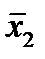
| 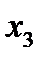
| 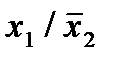
| 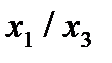
| 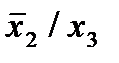
| 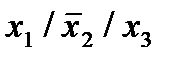
|
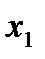
| 
| 
| 
| 
| 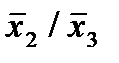
| 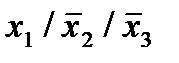
|
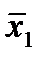
| 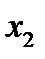
| 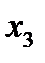
| 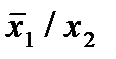
| 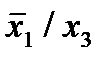
| 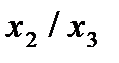
| 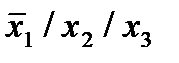
|
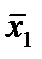
| 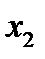
| 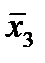
| 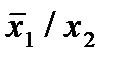
| 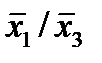
| 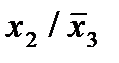
| 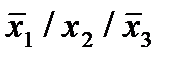
|
| 
| 
| 
| 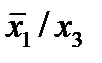
| 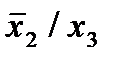
| 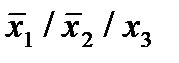
|
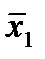
| 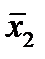
| 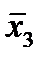
| 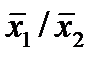
| 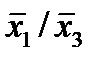
| 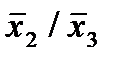
| 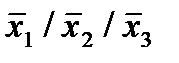
|
Отметим в последнем столбце те конъюнкции, которые входят в СНФ данной функции. Вычеркнем неотмеченные строки, затем вычеркнем в остальных строках (действуя по столбцу) те элементы, которые попали в вычеркнутые строки. В 3-ем столбце положим 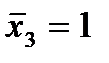 , при этом остальные элементы строк 2, 4, 6, 8, где стоит элемент
, при этом остальные элементы строк 2, 4, 6, 8, где стоит элемент 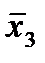 , положим равными нулю. В столбце 6 положим элемент
, положим равными нулю. В столбце 6 положим элемент 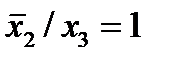 , следовательно, получим МНФ данной функции в виде:
, следовательно, получим МНФ данной функции в виде:
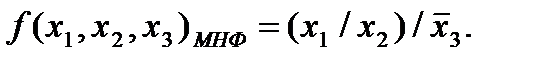
Ответ: 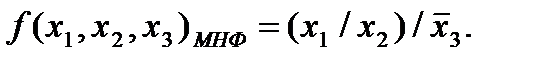
Метод Квайна:
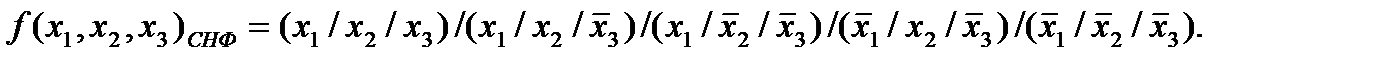
Для удобства вычисление построим таблицу и сделаем в ней преобразования, опирась на ранее изложенный алгоритм:
Члены 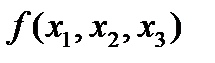
| Результат 1-го склеивания | Результат 2-го склеивания | |
| 1. | 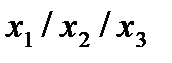 * *
| 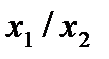 (1,2) (1,2)
| 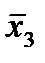 (2,5) (2,5)
|
| 2. | 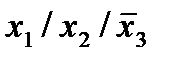 * *
| 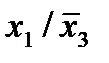 * (2,3) * (2,3)
| 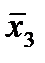 (3,4) (3,4)
|
| 3. | 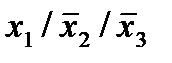 * *
| 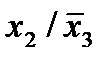 * (2,4) * (2,4)
| |
| 4. | 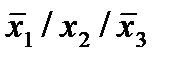 * *
| 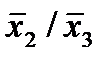 * (3,5) * (3,5)
| |
| 5. | 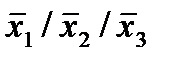 * *
| 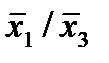 * (4,5) * (4,5)
|
Исходя из результатов получаем МНФ функции: 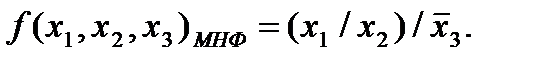
 2015-08-13
2015-08-13 617
617