Определение нагрузок на штанги и станок-качалку

Общая нагрузка на верхнюю часть колонны насосных штанг и на головку балансира станка-качалки в процессе работы насос­ной установки складывается из следующих' основных сил:

1) статических нагрузок от силы тяжести жидкости и штанг,
а также от сил трения плунжера в цилиндре и штанг о трубы;

2) силы инерции движущихся масс, возникающей при движении
колонны штанг и столба жидкости в результате переменных ускоре­
ний движения шатунно-кривошшшого механизма станка-качалки;

3) динамических нагрузок, создаваемых колебательными про­
цессами (вибрацией) в штангах.

Не все из перечисленных усилий поддаются точному учету. Практическое значение имеют суммарные максимальные и мини­мальные нагрузки на штанги. Величину этих нагрузок в работаю­щей установке с достаточной для практики точностью можно опре­делить при помощи специальных приборов — динамографов. Вместе с тем весьма важно уметь хотя бы приближенно подсчитывать на­грузки на штанги, чтобы оценивать их влияние на работу насосной установки. Основным элементом суммарной нагрузки на штанги ¹ являются статические нагрузки. При ходе плунжера вверх штанги находятся под действием собственной силы тяжести и силы тяжести жидкости в трубах над плунжером. При движении вниз штанги испытывают только действие собственной силы тяжести.

Следовательно, максимальные статические нагрузки будут при ходе вверх (в точке подвеса штанг):

Л,т = Лк + ^г, (152

где Р_ж — сила тяжести жидкости, находящейся над плунжером;

иг — сила тяжести штанг в жидкости.

: Пренебрегая разгружающей силой давления на плунжер снизу
сравнительно небольшого столба жидкости в межтрубном простран­
стве, уравнение (152) можно переписать в виде: "^

Р^ЗцЬй + ЯтЬЬь (153;

| где д_ж — масса 1 м столба жидкости с поперечным сечением, рав-| аым сечению плунжера; д_шт — масса 1 м штанг (с муфтами) в

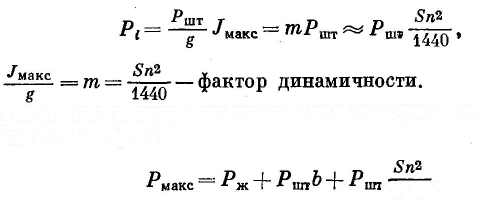На практике отношение радиуса кривошипа г к длине шатуна I составляет от */4 Д° V?- При г/1 = х/4 из (156) получим

(157)

где

С учетом сил инерции максимальная нагрузка на балансир в точке подвеса штанг будет (158)

воздухе; Ь — длина штанг; Ъ — коэффициент, учитывающий умень­шение массы штанг в жидкости, равный ^Л-Е) (здесь р_х ир — плот-

Р1 ности материала штанг и жидкости).

Фактические нагрузки несколько больше из-за силы трения. Трение штанг о трубы происходит в жидкости, но так как поверх­ность труб и штанг шероховатая, то для приближенных расчетов можно считать, что оно близко к трению сухой стали о сталь. Для этих условий силы трения штанг о трубы составляют менее 2% от силы тяжести штанг (для нормальных скважин, кривизна ко­торых не превышает 5—6°), поэтому ими можно пренебречь. Силы трения плунжера в цилиндре насоса также малы, и их можно не учитывать.

В наклонных и кривых скважинах силы трения могут составлять в общем балансе нагрузок значительно больше 2% от силы тяжести штанг и пренебречь ими нельзя. Аналитически силы трения в искрив­ленных и наклонных скважинах из-за наличия многих неизвестных факторов, связанных со сложным профилем ствола,-определить весьма трудно. Поэтому все расчеты максимальных нагрузок на штанги, проведенные без учета сил трения, справедливы только для верти­кальных скважин и скважин с небольшим углом наклона (5—6°).

Силы инерции движущихся масс определяют, исходя из следую­щих соображений.

Согласно элементарной теории кривошшшо-шатунного механизма, максимальное ускорение точки подвеса штанг будет при начале хода штанг вверх; оно определяется формулой

(154)

где 5 — двойная амплитуда качаний головки балансира (длина хода сальникового штока); со = яга/30 — угловая скорость вращения кривошипа; п — число качаний балансира в минуту; г — радиус кривошипа; / — длина шатуна.

По найденной величине ускорения максимальную нагрузку от силы инерции можно определить по формуле

(156)

(155)

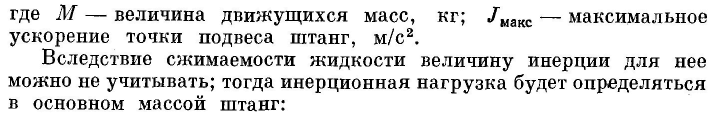
' 1440 '

где Р_шт Ь — сила тяжести штанг в жидкости; 5, п — длина хода и число ходов сальникового штока.

Работами советских исследователей (А. Н. Адонина, А. С. Вир-новского, И. А. Черного) показано, что формулой (158) для расчета максимальных усилий в штангах можно пользоваться лишь при сравнительно небольших глубинах спуска насоса и числах ходов. При больших глубинах спуска и большом числе ходов приведенная выше зависимость несправедлива. Объясняется это тем, что при больших глубинах и большом числе ходов возникают динамические нагрузки от вибрации штанг, которые накладываются на инерцион­ные усилия. По расчетам А. Н. Адонина, приведенными формулами можно пользоваться только до определенных значений параметра

Ф = —— (где а = 5100 м/с — скорость звука в материале штанг),

а

лежащих в пределах ф = 0,4-^- 0,45. Такие режимы откачки принято называть статическими.

При ф >0,45 режимы откачки называются динамическими, так как при величине параметра ф > 0,45 в системе усиливаются допол­нительные динамические нагрузки из-за колебательных процессов в штангах.

Аналитически точно определить динамические нагрузки с учетом колебательных процессов в штангах из-за сложности явлений трудно, поэтому для расчетов многими исследователями предложены при­ближенные формулы (формулы А. С. Вирновского, А. И. Адонина, И. А. Чарного), которые опубликованы в специальной литературе.