Существует два способа реализации ВМНК (WLS) в пакете Gretl:
1. При выборе из главного меню команды Model\Other Linear Models\Weighted Least Squares ….(рисунок 12) открывается окно спецификации модели, которое предусматривает выбор из списка переменных открытого набора переменной - веса w. Данная переменная добавляется к набору путём ввода данных вручную или определяется путём ввода соответствующей формулы. Данный способ используется если дисперсия ошибки 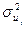 или известна или неизвестна, но существует соотношение между ней и одной из объясняющих переменных (
или известна или неизвестна, но существует соотношение между ней и одной из объясняющих переменных (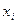 ), например,
), например, 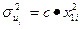 .
.
- При выборе из главного меню команды Model\Other Linear Models\Heteroskedasticity Corrected… ( рисунок 12) веса наблюдений (wi) определяются Gretl по формуле (4) и не вводятся пользователем. В качестве условия корректности применения рассматриваемого метода оценивания рассматривается получение нормального распределения остатков. Форму распределения можно проверить при помощи команды меню окна результатов моделирования Tests\normality of residual…..
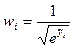 , (4)
, (4)
где 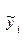 - модельные значения зависимой переменной, полученные при использовании 1МНК; e=2,718..; wi -вес i-го наблюдения.
- модельные значения зависимой переменной, полученные при использовании 1МНК; e=2,718..; wi -вес i-го наблюдения.
|
|
|
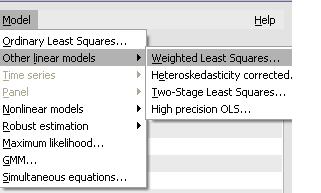
Рисунок 12 – Способы реализации ВМНК (WLS) в пакете Gretl
Обратимся к вышеприведённому примеру набора данных bwages.gdt для иллюстрации обоих способов оценивания регрессионной модели 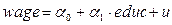 методом ВМНК.
методом ВМНК.
Этап 1. Введём новую переменную – вес w, которая будет определяться по формуле 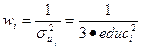 .
.
Для этого выберем команду Define new variable из меню Variable (рисунок 13).
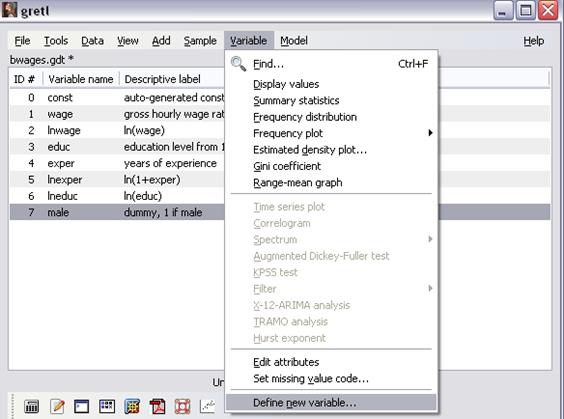
Рисунок 13 – Создание новой переменной
В открывшемся окне “add var” введём имя переменной w и нажмём ОК, в появившемся окне «edit data» не вводим значения переменной, а нажимаем кнопку «close» для создания переменной с пустыми значениями (рисунок 14).

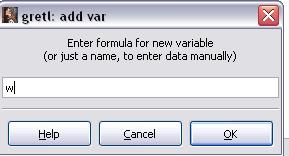
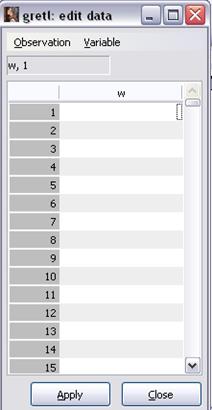
Рисунок 14 – Ввод имени переменной
Данная переменная w c пустыми значениями и без описания появится в списке открытого набора данных. Введём описание переменной, обратившись к команде Variable\Edit Attributes.
В открывшемся окне (рисунок 15) введём в поле “Description” описание «weights» (веса) и нажмём ОК.
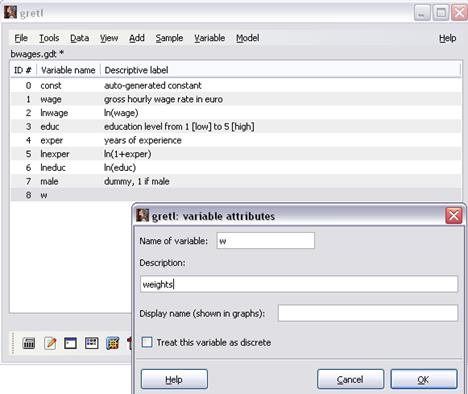
Рисунок 15 – Изменение атрибутов переменной
Введём формулу для переменной w, повторно обратившись к команде Variable\Edit Attributes. Теперь в поле“Description” вместо описания «weights» введём формулу =1/(3*educ^2) (рисунок 16).
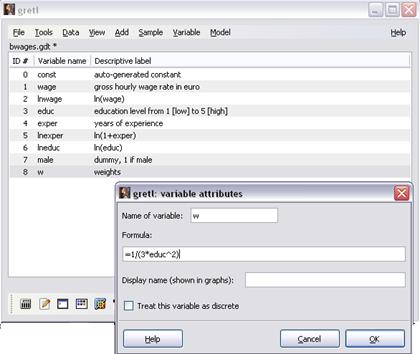
Рисунок 16 – Ввод формулы для определения переменной w
Этап 2. Просмотрим значения созданной переменной w, выбрав её в списке щелчком мыши и обратившись к команде Data\Display Values (или двойным щелчком мыши по её названию в списке) (рисунок 17).
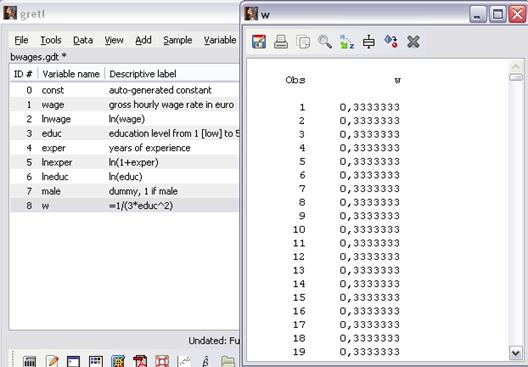
Рисунок 17 – Просмотр значений переменной w
Этап 3. Для оценки модели 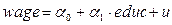 методом ВМНК (OLS) выполним команду Model\Other Linear Models\Weighted Least Squares ….(рисунок 18) и в открывшемся окне спецификации модели (рисунок 19) выберем при помощи кнопок «Choose» и «Add» переменные: wage (з.пл) - зависимая переменная; w – веса наблюдений; educ (уровень образования) – независимая переменная.
методом ВМНК (OLS) выполним команду Model\Other Linear Models\Weighted Least Squares ….(рисунок 18) и в открывшемся окне спецификации модели (рисунок 19) выберем при помощи кнопок «Choose» и «Add» переменные: wage (з.пл) - зависимая переменная; w – веса наблюдений; educ (уровень образования) – независимая переменная.
|
|
|
Рисунок 18 – Реализация ВМНК (OLS) в Gretl
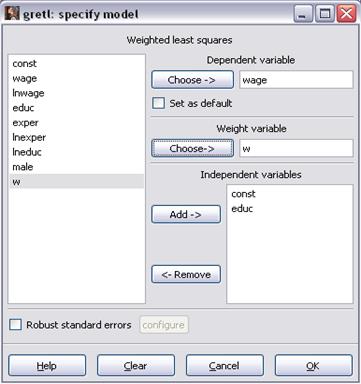
Рисунок 19 – Оценивание модели 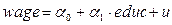 при помощи ВМНК (OLS)
при помощи ВМНК (OLS)
Результаты оценивания представлены в окне результатов моделирования (рисунок 20).
|
|
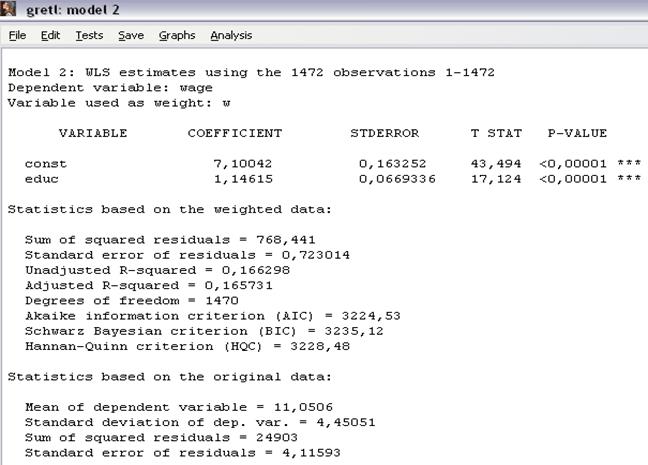
Рисунок 20 – Результаты оценивания модели 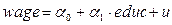 методом ВМНК (WLS)
методом ВМНК (WLS)
Сравнивая модели, полученные методом ВМНК 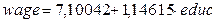 (рисунок 20) и методом 1МНК
(рисунок 20) и методом 1МНК 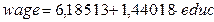 (рисунок 7) можно сделать вывод о том, что при использовании 1МНК оценка коэффициента
(рисунок 7) можно сделать вывод о том, что при использовании 1МНК оценка коэффициента 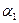 была завышена, а оценки
была завышена, а оценки 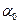 и T-STAT – занижены, но на правильности решения о принятии альтернативной гипотезы это не отразилось (значения P-VALUE не изменились).
и T-STAT – занижены, но на правильности решения о принятии альтернативной гипотезы это не отразилось (значения P-VALUE не изменились).
Этап 4. Воспользуемся вторым способом оценки модели 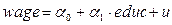 методом ВМНК (OLS), выполнив команду Model\Other Linear Models\Heteroskedasticity Corrected… (рисунок 21).
методом ВМНК (OLS), выполнив команду Model\Other Linear Models\Heteroskedasticity Corrected… (рисунок 21).
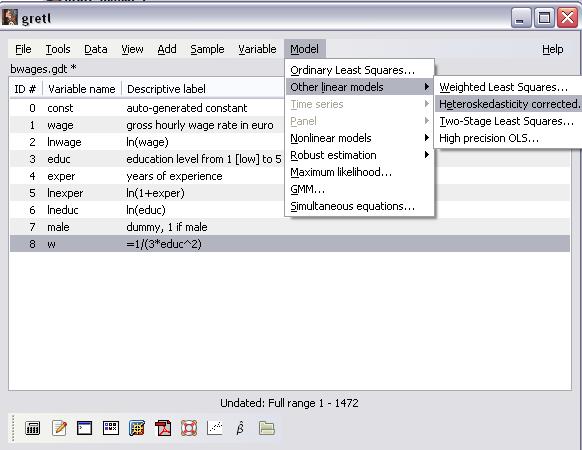
Рисунок 21 – Альтернативный способ оценки модели методом ВМНК (WLS)
Заполним окно спецификации также, как на предыдущем этапе за исключением ввода переменной – веса w, и нажмём кнопку ОК (рисунок 22).
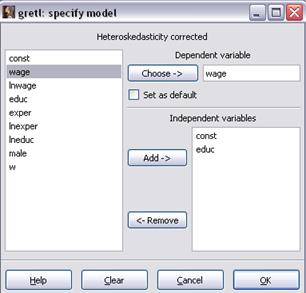
Рисунок 22 – Оценивание модели 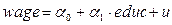 при помощи ВМНК (OLS) c автоматическим определением весов наблюдений
при помощи ВМНК (OLS) c автоматическим определением весов наблюдений
Сравнивая полученную модель 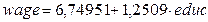 (рисунок 23) с моделью, оцененною с применением 1МНК
(рисунок 23) с моделью, оцененною с применением 1МНК 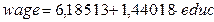 (рисунок 7) можно отметить расхождения в значениях показателей регрессионной таблицы, но на правильности решения о принятии альтернативной гипотезы это также не отразилось (значения P-VALUE не изменились).
(рисунок 7) можно отметить расхождения в значениях показателей регрессионной таблицы, но на правильности решения о принятии альтернативной гипотезы это также не отразилось (значения P-VALUE не изменились).
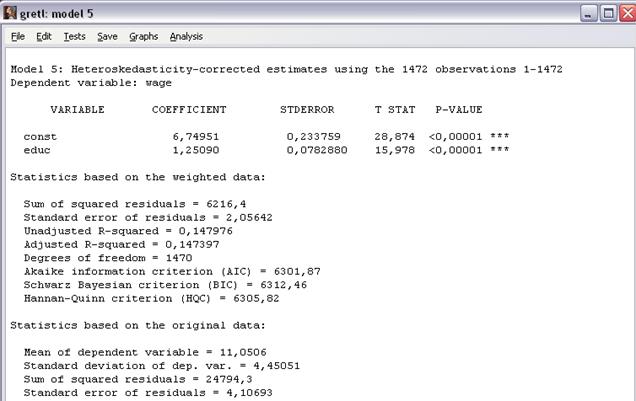
Рисунок 23 – Результаты оценивания модели 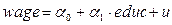 методом ВМНК (WLS) с автоматическим определением весов наблюдений
методом ВМНК (WLS) с автоматическим определением весов наблюдений
Проверим условие корректности применения рассматриваемого метода –получение нормального распределения остатков, - обратившись к команде Tests\normality of residual… меню окна модели (рисунок 23).
Рисунок 24 показывает, что данное условие не соблюдается P-value=0,0000, что меньше уровней значимости 1% и 5%, поэтому отвергаем нулевую гипотезу о нормальности распределения остатков.
Вывод: В результате исследования 1479 бельгийских семей выявлена прямая зависимость заработной платы (wage) от уровня образования (educ). Наилучшей моделью, описывающей рассматриваемую зависимость, является модель 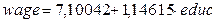 , полученная методом ВМНК (WLS) с заданием пользователем весов наблюдений.
, полученная методом ВМНК (WLS) с заданием пользователем весов наблюдений.
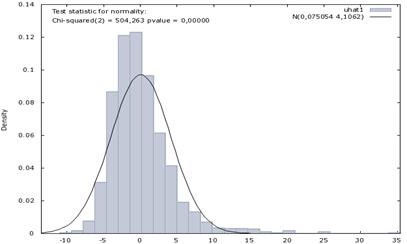
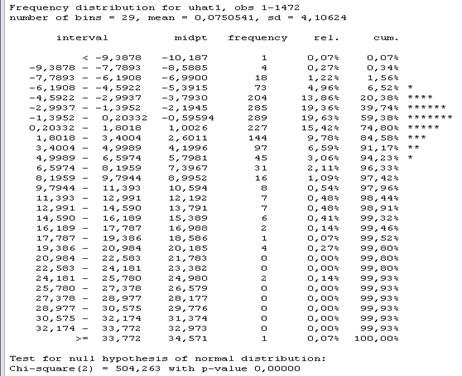
Рисунок 24 – Результаты теста на нормальность распределения остатков модели 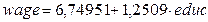
 2015-08-13
2015-08-13 2743
2743








