якщо потрібно обчислити лише деякі з власних значень (наприклад, 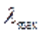 або
або 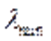 ), то найпростіше використати степеневий метод для формування послідовності векторів
), то найпростіше використати степеневий метод для формування послідовності векторів
(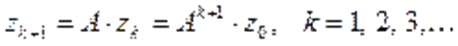 11)
11)
Нехай матриця А має n лінійно незалежних векторів 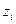 і максимальне за величиною власне значення
і максимальне за величиною власне значення 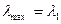 таке, що
таке, що 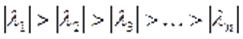 .
.
Якщо розкласти деякий ненульовий вектор 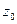 за базисом власних векторів матриці
за базисом власних векторів матриці
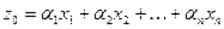 ,
,
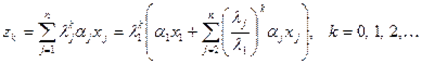
Оскільки 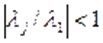 для
для 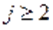 , напрям вектора
, напрям вектора 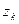 прямує до напряму власного вектора
прямує до напряму власного вектора 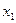 , якщо тільки
, якщо тільки 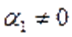 .
.
Для підвищення стійкості обчислень проводять масштабування послідовності векторів 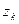 , яке найпростіше здійснити, якщо перейти до послідовності
, яке найпростіше здійснити, якщо перейти до послідовності 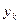 нормуванням векторів
нормуванням векторів 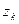 за значенням їх найбільших елементів
за значенням їх найбільших елементів 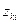 , тобто замість виразу (11) використовувати співвідношення:
, тобто замість виразу (11) використовувати співвідношення:
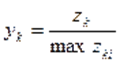 ,
, 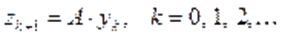 , (12)
, (12)
при цьому
 (13)
(13)
і похибка обчислення найбільшого власного значення прямує до нуля як 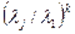 .
.
Якщо степеневий метод застосувати до оберненої матриці  , то аналогічно можна оцінити величину мінімального власного значення
, то аналогічно можна оцінити величину мінімального власного значення 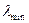 , якщо виконується умова
, якщо виконується умова 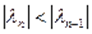 . При цьому мінімальне власне значення матриці А обчислюється за формулою
. При цьому мінімальне власне значення матриці А обчислюється за формулою
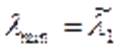 , де
, де 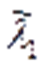 – максимальне за модулем власне значення матриці
– максимальне за модулем власне значення матриці 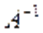 .
.
11. 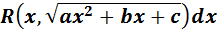
Інтеграли такого типу обчислюються за допомогою підстановки Ейлера, так підстановки t третього типу
1) А>0 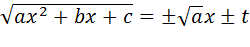
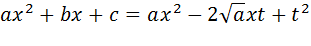
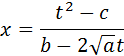
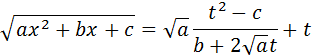
 2015-08-13
2015-08-13 411
411







