Визначений інтеграл з верхньою змінною межею, його властивості

Нехай на 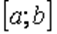задана неперервна функція 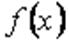. Ця функція інтегрована на будь-якому відрізку 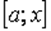, де 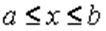. Отже, існує 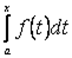, який називається визначеним інтегралом із змінною верхньою межею. Позначимо його через .

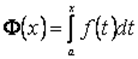Властивість 1. Постійний множник можна виносити за знак визначеного інтегралу: якщ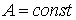о , то

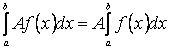. (3.1)

Доведення. .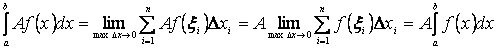

Властивість 2. Визначений інтеграл від алгебраїчної суми декількох функцій рівний алгебраїчній сумі інтегралів від доданків

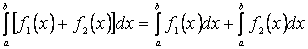. (3.2)

Доведення.

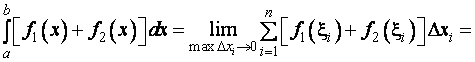
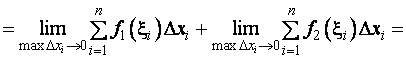
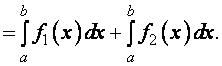
Властивість 1 і 2 хоч і доведені для випадку 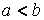, залишаються в силі і при .

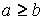Властивість 3. Якщо на відрізку 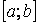де 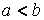, функці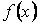ї і 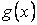задовольняють умові 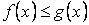, то

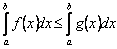. (3.3)

Доведення. Розглянемо різницю:

.

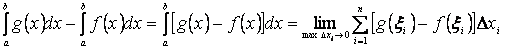Але для 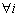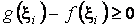і 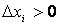. Отже 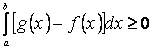. Звідси отримаємо (3).

Якщо 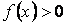і 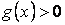, то можна дати геометричну інтерпретацію