Тригон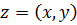ометрическая форма

Так как определяется как пара действительных чисел, то естественной геометрической интерпретацией является изображение комплексного числа точкой 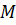некоторой плоскости с координатами .

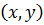Такую плоскость называют комплексной, ось абсцисс – действительной осью, ось ординат – мнимой осью. При этом устанавливается взаимно-однозначное соответствие между множеством всех комплексных чисел 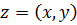и множеством точек 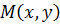или множеством радиус-векторов .

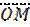у

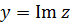
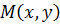
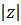
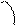
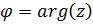х

О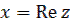

Рис. 1.

Введем на плоскости 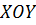полярные координаты 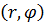. Длина вектора 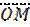называется модулем комплексного числа 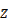и обозначается 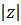или 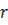: 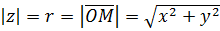(см. рис.1).

Опр. – Угол 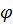между радиус-вектором 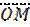и положительным направлением

оси 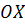называются аргументом комплексного числа .

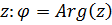Угол 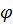определяется неоднозначно, с точностью до слагаемого 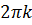. Удобно работать с приведенным аргументом 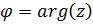, 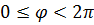(либо

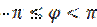). Для числа 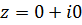аргумент не определён. При этом аргумент комплексного числа определяется следующим образом:

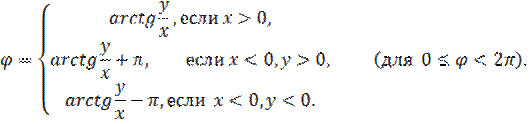
Практически, для определения 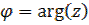решают систему уравнений 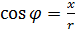, 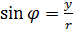и изображают 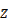вектором, чтобы определить, в каком квадрате плоскости лежит точка.

Так как 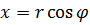, , 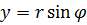то комплексное число 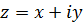можно записать в следующем виде: .

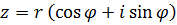Выражение вида 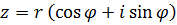называют тригонометрической формой записи комплексного числа.

Показательная форма

Используя формулу, полученную Эйлером: 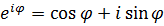, можно получить еще одну, показательную форму комплексного числа: .

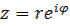Выражение вида 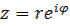называют показательной формой записи комплексного числа.

Для комплексно – сопряженного числа получаем: .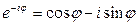

Комбинируя 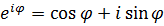и 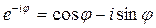, можно получить выражения .

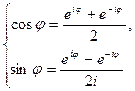Для комплексных чисел в показательной форме будут справедливы следующие свойства:

1)

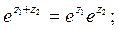
2)

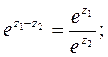
3) 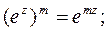где m – целое число.