Основные действия с комплексными числами вытекают из его определения и схожи с действиями над многочленами.
1) Сложение и вычитание.
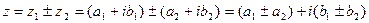
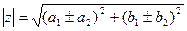
2) Умножение.
| В алгебраической форме | В тригонометрической форме | В показательной форме |
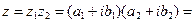
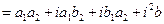
| 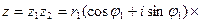
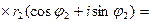
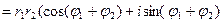
| 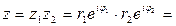
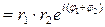
|
| В случае комплексно – сопряженных чисел | ||
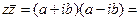
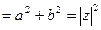
| 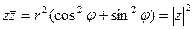
|
3) Деление.
| В алгебраической форме | В тригонометрической форме | В показательной форме |
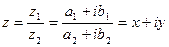
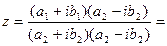
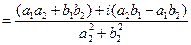 или или 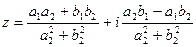
|
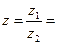
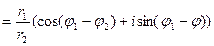
| 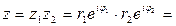
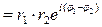
|
4) Возведение в степень.
Из операции умножения комплексных чисел следует, что
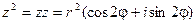
В общем случае получим:
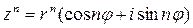 , (1)
, (1)
где n – целое положительное число.
Выражение (1) называется формулой Муавра.
(Абрахам де Муавр (1667 – 1754) – английский математик)
Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.
Пример. Вывести формулы sin2 j и cos2 j.
Решение.
Рассмотрим некоторое комплексное число 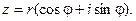
Тогда с одной стороны 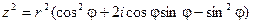 .
.
По формуле Муавра: 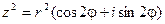
Приравнивая, получим 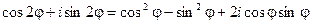
Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то
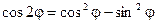
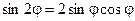
Получили известные формулы двойного угла.
5) Извлечение корня из комплексного числа.
Аналогичная формула применима также и при вычислении корней 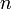 -ой степени из ненулевого комплексного числа:
-ой степени из ненулевого комплексного числа:
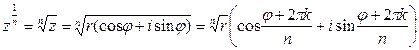 ,
,
где 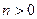 ,
, 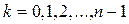 .
.
Отметим, что корни 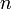 -й степени из ненулевого комплексного числа всегда существуют, и их количество равно
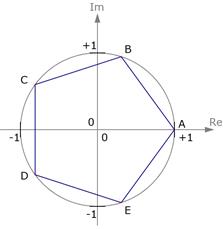
-й степени из ненулевого комплексного числа всегда существуют, и их количество равно 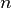 различных значений. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного
различных значений. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного 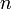 -угольника, вписанного в окружность радиуса
-угольника, вписанного в окружность радиуса 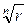 с центром в начале координат (см. рис.2).
с центром в начале координат (см. рис.2).
 2015-08-13
2015-08-13 614
614








