Корнем называется всякий элемент поля, значение многочлена на котором равно нулю. Полином степени m имеет ровно m корней (с учётом кратности), принадлежащих некоторому расширенному полю 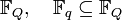 . Если
. Если 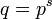 , где
, где 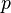 — простое, то
— простое, то 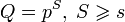 . Исходя из свойств конечных полей, любой элемент поля
. Исходя из свойств конечных полей, любой элемент поля 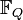 является корнем двучлена
является корнем двучлена 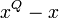 . Таким образом, корни многочлена
. Таким образом, корни многочлена 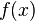 также являются корнями двучлена
также являются корнями двучлена 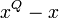 .
.
Справедливы теорема Безу и следствия из неё:
Остаток от деления 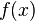 на на 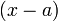 равен равен 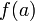 . .
|
Если 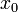 — корень — корень 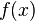 , то , то 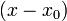 делит делит 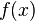 . .
|
Если 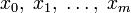 суть корни суть корни 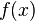 , то , то
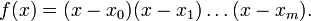
|
Также справедлива следующая теорема:
Теорема 1. Если 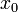 — корень — корень 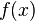 , то , то 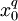 — тоже корень — тоже корень 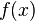 . .
|
Часть 2. Практика:
 2015-08-13
2015-08-13 388
388








