Материал из Википедии — свободной энциклопедии
Многочленом 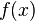 над конечным полем
над конечным полем 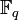 называется формальная сумма вида
называется формальная сумма вида
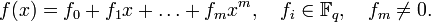
Здесь 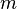 — целое неотрицательное число, называемое степенью многочлена
— целое неотрицательное число, называемое степенью многочлена 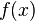 , а
, а 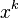 — элементы алгебры над
— элементы алгебры над 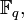 умножение которых задаётся правилами:
умножение которых задаётся правилами:
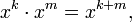
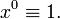
Такое определение позволяет умножать многочлены формально, не заботясь о том, что разные степени одного и того же элемента конечного поля могут совпадать.
Связанные определения
· Число 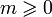 называется степенью полинома и обозначается как
называется степенью полинома и обозначается как 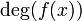 .
.
· Если 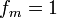 , то полином называется нормированным или унитарным. Полином всегда можно нормировать делением его на коэффициент
, то полином называется нормированным или унитарным. Полином всегда можно нормировать делением его на коэффициент 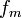 при старшей степени.
при старшей степени.
· Сумма и произведение полиномов определены обычным образом, а операции с коэффициентами осуществляются в поле 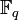 .
.
· Для двух полиномов 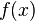 и
и 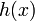 таких, что
таких, что 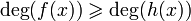 , всегда найдутся полиномы
, всегда найдутся полиномы 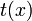 и
и 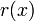 над полем
над полем 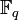 , что будет выполняться соотношение
, что будет выполняться соотношение
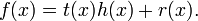
· Если степень 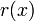 строго меньше степени
строго меньше степени 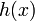 , то такое соотношение называется представлением полинома
, то такое соотношение называется представлением полинома 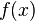 в виде частного и остатка от деления
в виде частного и остатка от деления 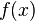 на
на 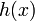 , причем такое представление единственно. Ясно, что
, причем такое представление единственно. Ясно, что 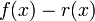 делится без остатка на
делится без остатка на 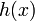 , что записывается как
, что записывается как 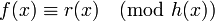 .
.
· Полином 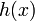 называется делителем полинома
называется делителем полинома 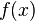 , если
, если 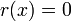 .
.
· Полином является неприводимым над полем 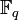 , если он не имеет нетривиальных делителей (степени большей 0 и меньшей
, если он не имеет нетривиальных делителей (степени большей 0 и меньшей 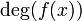 ).
).
 2015-08-13
2015-08-13 1202
1202








