Для этой цели удобно в использовании операционного преобразования Лапласа. Под прямым преобразованием Лапласа понимается переход от рассмотрения функции действительного аргумента 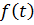 к рассмотрению функции комплекса.
к рассмотрению функции комплекса.
Где, Р - комплексное число.
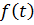 – оригинал; F(P) – изображение;
– оригинал; F(P) – изображение;
Р=α+jβ
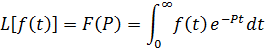
Многие операции под их оригиналом.
Свойства Лапласа.
Свойство линейности. Преобразование Лапласа от произведения постоянного числа на оригинал = произведению этого числа на изображение оригинала.
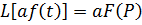
Свойство дифференцирования. Преобразование Лапласа от произведения = произведению комплексного числа на оригинал.
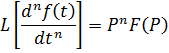
Свойство интегрирования.
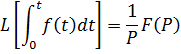
Пример использования этих преобразований.
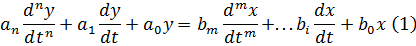
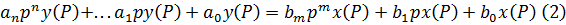
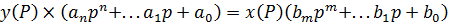
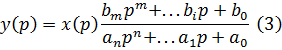
По известному входному воздействию х(t) по табл. Лапласа ищем его изображение х(р) и подставляем в уравнение (3), получая при этом у(р) в общем виде. Далее по полученному у(р) по тем же табл. Ищем его оригинал у(t), что является решением уравнения.
Под передаточной функции звена или системы понимается отношение изображения выходной величины к входной.
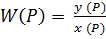 - основное определение автоматики.
- основное определение автоматики.
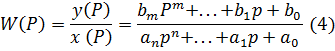
Не трудно заметить, что передаточная функция не зависит от входных и выходных величин, а определяется только видом уравнения динамики и его коэффициентом.
Пр.: 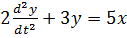 Найти передаточную функцию.
Найти передаточную функцию.
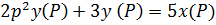
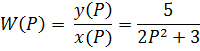
Пример:
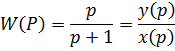
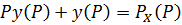
Второе свойство Лапласа.
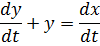
 2015-08-13
2015-08-13 567
567








