Сложение взаимно перпендикулярных колебаний

Пусть материальная точка может совершать колебания, как вдоль оси 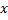, так и вдоль оси 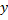. Если возбудить оба колебания, материальная точка будет двигаться по некоторой криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнение колебаний запишутся следующим образом:

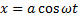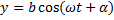, , где α - разность фаз обоих колебаний.

Выражения представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить уравнений параметр t. Следовательно,

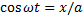
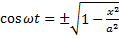
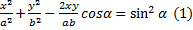уравнение эллипса, оси которого повернуты относительно координатных осей .

Определим форму траектории для некоторых частных случаев.

1. Разность фаз α равна нулю. В этом случае уравнение (1) принимает вид

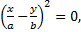откуда получается уравнение прямой

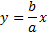
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω

И амплитудой, равной .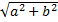

2. Разность фаз α равна 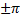. Уравнение (1) имеет вид

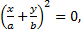откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой.

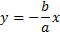
3. При 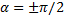уравнение (1) переходит в

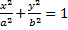, т.е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний.

В моменты t=0 тело находится в точке 1. В следующие моменты времени координата 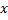уменьшается, а координата 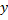становится отрицательной.

Следовательно, движение совершается по часовой стрелке.

Если частоты взаимно перпендикулярных колебаний одинаковы, то траектория результирующего движения имеет сложный вид кривых, называемых Лиссажу.

Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее фигура Лиссажу. На рисунке показана кривая для отношения частот 3:4 и разности фаз .