№1. Наити производную функции: 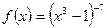
Решение: Будем рассматривать данную функцию как сложную, где. Тогда, согласно 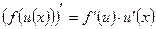 , получим
, получим 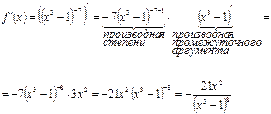
№2. Найти производную функции 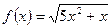 .
.
Решение: Будем рассматривать данную функцию как сложную, составленную из функций 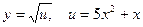 . Тогда, согласно
. Тогда, согласно 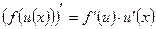 , получим
, получим 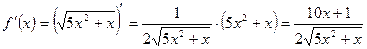
№3. Найдите производную функции: 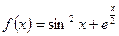
Решение: Последовательно определим, от какого выражения берется производная:
- сначала берется производная суммы;
- затем для каждого из слагаемых используется правило вычисления производной сложной функции.
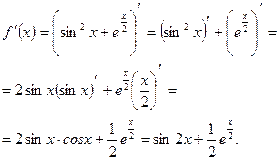
 2015-08-13
2015-08-13 353
353








