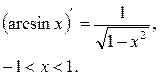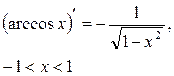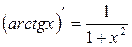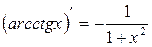Пусть 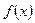 - непрерывная функция, монотонная на интервале
- непрерывная функция, монотонная на интервале 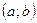 . Тогда, функция
. Тогда, функция 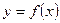 имеет обратную функцию
имеет обратную функцию 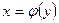 , которая также является непрерывной и монотонной функцией на интервале
, которая также является непрерывной и монотонной функцией на интервале 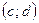 , в который функция f переводит интервал
, в который функция f переводит интервал 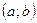 . Пусть
. Пусть 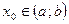 - фиксированная точка и
- фиксированная точка и 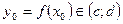 -- точка, ей соответствующая. Тогда
-- точка, ей соответствующая. Тогда 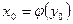 .
.
Теорема 4.5. Пусть функция 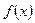 имеет в точке
имеет в точке 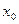 производную
производную 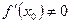 . Тогда обратная функция
. Тогда обратная функция 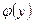 имеет в соответствующей точке
имеет в соответствующей точке 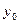 производную
производную 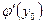 , которую можно отыскать по формуле
, которую можно отыскать по формуле
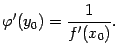
|
 2015-08-13
2015-08-13 407
407