Подвiйнiсть властивостей мiкрочастинок – рiзка вiдмiннiсть їх вiд частинок класичної фiзики. Ця якiсна вiдмiннiсть вимагає описувати їх рух за iншими законами, нiж у класичнiй фiзицi. Хвильовi властивостi показують, що їх рух пiдкоряється законам розповсюдження хвиль де Бройля. Тому хвильовi процеси описуються хвильовим рiвнянням, яке для мiкрочастинок виведено Шредiнгером. Його сенс: рух у силовому полi мікрочастинки, що володiє потенцiальною енергiєю 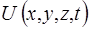 , пiдкоряється хвильовому рiвнянню виду:
, пiдкоряється хвильовому рiвнянню виду:
 . (5)
. (5)
Рiшення (5) – хвильова функцiя 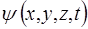 . Рiвняння Шредiнгера задовольняється тiльки комплексними хвильовими функцiями. Тобто фiзичний смисл має не
. Рiвняння Шредiнгера задовольняється тiльки комплексними хвильовими функцiями. Тобто фiзичний смисл має не 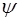 , а добуток її на комплексно спряжену з нею
, а добуток її на комплексно спряжену з нею 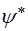 . Цей добуток дiйсний та пропорцiйний iмовiрностi знаходження мiкрочастинки у момент часу t у видiленому елементi об'єму
. Цей добуток дiйсний та пропорцiйний iмовiрностi знаходження мiкрочастинки у момент часу t у видiленому елементi об'єму 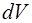 :
:
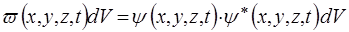 . (6)
. (6)
Властивостi 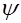 за її фiзичним смислом:
за її фiзичним смислом:
1. Неперервна та має неперервну першу похідну.
2. Однозначна та кiнцева у всiх точках простору (тому що не може iмовiрнiсть знаходження мiкрочастинки у тому або iншому елементi 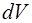 мiнятися стрибкоподiбно вiд точки до точки або бути неоднозначною та нескiнченною).
мiнятися стрибкоподiбно вiд точки до точки або бути неоднозначною та нескiнченною).
Iнтеграл 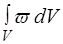 від (6), узятий по усьому простору
від (6), узятий по усьому простору 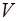 , дорiвнює одиницi, тому що вiдбиває вірогідний факт – мікрочастинка є у цьому просторi:
, дорiвнює одиницi, тому що вiдбиває вірогідний факт – мікрочастинка є у цьому просторi:
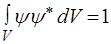 . (7)
. (7)
Це – умова нормiровки; функції 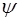 , що складають (7), – нормованi функцiї.
, що складають (7), – нормованi функцiї.
Рiвняння Шредiнгера описує усю еволiцiю стану мiкрочастинки. Закон її руху визначається завданням 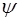 у кожний момент часу у кожнiй точцi простору.
у кожний момент часу у кожнiй точцi простору.
Амплiтудне рiвняння Шредiнгера. Потенцiйна енергiя 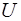 у (5) – функцiя координат та часу. Але на практицi часто
у (5) – функцiя координат та часу. Але на практицi часто 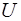 – функцiя координат та не залежить вiд часу. Тому запишемо повну функцію у вигляді:
– функцiя координат та не залежить вiд часу. Тому запишемо повну функцію у вигляді:
 . (8)
. (8)
За такої умови розглянемо о дновимiрний випадок, тобто рух мiкрочастинки повздовж осi 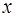 . Рiвняння Шредiнгера (5) при цьому матиме вигляд:
. Рiвняння Шредiнгера (5) при цьому матиме вигляд:
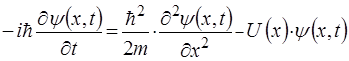 . (9)
. (9)
Вираз (8) стане:
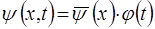 . (10)
. (10)
Пiдставимо (10) у (9), поділивши результат на (10), та зробимо розподіл змінних 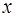 і
і 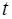 :
:
 .
.
Змiннi розподiленi: лiворуч – функцiя вiд x, праворуч – вiд t.
Рiвнiсть можлива помiж ними при умовi рiвностi кожної частини однiй постiйнiй величинi. Такою величиною є 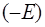 – повна енергiя частинки. Прирiвнюючи частини
– повна енергiя частинки. Прирiвнюючи частини 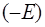 та перетворюючи рівність, одержимо:
та перетворюючи рівність, одержимо:
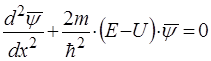 , (11)
, (11)
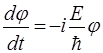 . (12)
. (12)
Рiвняння (11) у загальному трьохвимірному випадку буде мати вигляд:
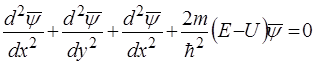 . (13)
. (13)
Сума других похiдних будь-якої функцiї – оператор Лапласа, що позначається 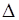 . Тодi (13) буде мати вигляд:
. Тодi (13) буде мати вигляд:
 . (14)
. (14)
Функцiя 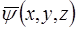 – амплiтуда хвильової функцiї
– амплiтуда хвильової функцiї 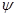 , а рiвняння (11), (13) та (14) – амплітуднi рiвняння Шредiнгера (що не мiстять у собi часу).
, а рiвняння (11), (13) та (14) – амплітуднi рiвняння Шредiнгера (що не мiстять у собi часу).
Коли мікрочастинка рухається у обмеженому просторi, тодi рiшення рiвняння Шредiнгера вiдповiдають умовам однозначностi, кiнцевостi та неперервностi тiльки за умови суворого визначення значень 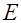 :
:  , якi звуться власними значеннями енергiї мiкрочастинки. Зв'язанi з ними хвильовi функцiї
, якi звуться власними значеннями енергiї мiкрочастинки. Зв'язанi з ними хвильовi функцiї 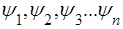 , звуться власними.
, звуться власними.
Роздивимося рiвняння (12). Iнтегруючи його, одержимо рiшення для одного iз власних значень енергiї 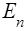 :
:
 . (15)
. (15)
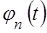 показує залежнiсть повної хвильової функцiї
показує залежнiсть повної хвильової функцiї 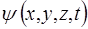 вiд часу. Iз (15) видно, що ця залежнiсть гармонiчна з частотою
вiд часу. Iз (15) видно, що ця залежнiсть гармонiчна з частотою  або
або 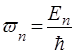 .
.
 2015-08-21
2015-08-21 278
278








