Рух вiльної частинки
Для цiлковито вiльної частинки, яка рухається уздовж осi 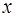 ,
, 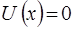 і рiвняння Шредiнгера (9) набуває такого вигляду:
і рiвняння Шредiнгера (9) набуває такого вигляду:
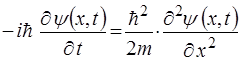 .
.  (21)
(21)
Рiшенням цього рiвняння буде:
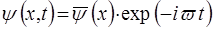 , (22)
, (22)
де 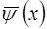 – хвильова функцiя, яка задовольняє амплiтудному рiвнянню Шредiнгера (11):
– хвильова функцiя, яка задовольняє амплiтудному рiвнянню Шредiнгера (11):
 . (23)
. (23)
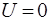 , тому Е являє собою кiнетичну енергiю частинки:
, тому Е являє собою кiнетичну енергiю частинки: 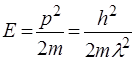 . Пiдставимо це у (23) і одержимо:
. Пiдставимо це у (23) і одержимо:
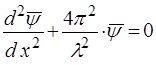 . (24)
. (24)
Позначимо: 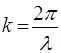 . Тодi:
. Тодi:
 . (25)
. (25)
Окремими рiшеннями рiвняння (25) будуть:
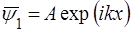 та
та 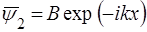 , (26)
, (26)
де 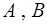 - постiйнi коефiцiєнти.
- постiйнi коефiцiєнти.
Спiльним рiшенням для (25) буде:
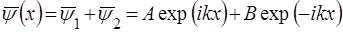 . (27)
. (27)
Помноживши обидвi частини цього рiвняння на 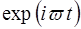 , одержимо рiшення рiвняння (21):
, одержимо рiшення рiвняння (21):
 . (28)
. (28)
Рiвняння (28) відображує суперпозицiю двох плоских хвиль, якi розповсюджуються у протилежних напрямках. Для частинки, яка рухається у позитивному напрямку осi 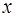 ,
, 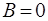 та
та
 . (29)
. (29)
Для частинки, що рухається протилежно осi 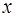 ,
, 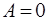 та
та
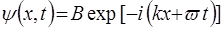 . (30)
. (30)
У випадку, коли напрям руху вiльної частинки не спiвпадає нi з однiєю iз осей координат, рiвняння Шредiнгера, яке описує цей рух, має такий вигляд:
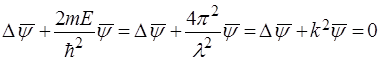 , (31)
, (31)
де 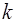 - вектор, що спiвпадає з напрямком розповсюдження хвиль де Бройля, а за абсолютною величиною дорiвнює:
- вектор, що спiвпадає з напрямком розповсюдження хвиль де Бройля, а за абсолютною величиною дорiвнює:
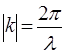 . (32)
. (32)
Цей вектор зветься хвильовим. Його компонентами по осях координат є 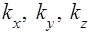 .
.
Рiшенням рiвняння (30) є хвильова функцiя
 , (33)
, (33)
яка являє собою рiвняння плоскої гармонiчної хвилi, що розповсюджується у напрямку вектора 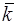 .
.
У цьому рiвняннi 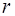 є радiус-вектором, проведеним у будь-яку точку фронту хвилi.
є радiус-вектором, проведеним у будь-яку точку фронту хвилi.
З порiвняння першого та третього виразу у (31) знаходимо:
 . (34)
. (34)
Таким чином, енергiя вiльної частинки пропорцiйна квадрату хвильового вектора. Графiк цiєї залежностi являє собою квадратичну парабулу (рис. 3). На 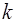 нiяких обмежень не накладається, тому вiльна частинка може володiти будь-якою енергiєю: її енергетичний спектр є суцiльним. Спiввiдношення (34) зветься дисперсiйною формулою.
нiяких обмежень не накладається, тому вiльна частинка може володiти будь-якою енергiєю: її енергетичний спектр є суцiльним. Спiввiдношення (34) зветься дисперсiйною формулою.
Фазова та групова швидкiсть
У рiвняннi плоскої хвилi (29), що розповсюджується уздовж осi 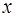 ,
,
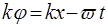 (35)
(35)
представляє собою фазу хвилi. Дiлянка хвилi, що має дане значення фази, перемiщується уздовж осi 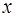 з визначеною швидкiстю, що зветься фазовою швидкiстю хвилi
з визначеною швидкiстю, що зветься фазовою швидкiстю хвилi 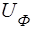 . Її можна визначити iз умови постiйностi фази:
. Її можна визначити iз умови постiйностi фази: 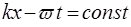 .
.

Рис. 3. Залежнiсть енергiї вільної мiкрочастинки
Е від хвильового вектора 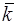 (дисперсiйна крива).
(дисперсiйна крива).
Диференцюючи за часом, знаходимо:
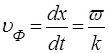 . (36)
. (36)
Пiдставимо сюди  та
та 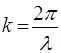 , одержимо:
, одержимо:
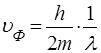 . (37)
. (37)
Iз (37) видно, що фазова швидкiсть хвиль де Бройля залежить вiд їх довжини, тобто має мiсце дисперсiя.
Суворо кажучи, монохроматична хвиля - фiзична абстракцiя. У будь-якому реальному випадку розповсюджується група хвиль, бiльш чи менш близьких за своєю довжиною та напрямком розповсюдження - хвильовий пакет.
Цей пакет розповсюджується з визначенною швидкiстю, що називається груповою швидкiстю 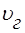 :
:
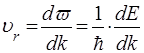 . (38)
. (38)
Для хвиль де Бройля  . Диференцюючи за
. Диференцюючи за 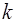 , одержимо:
, одержимо: 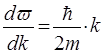 . Пiдставимо сюди
. Пiдставимо сюди  , будемо мати:
, будемо мати:
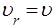 . (39)
. (39)
Формула (39) показує, що групова швидкiсть розповсюдження хвиль де Бройля дорiвнює швидкостi руху мiкрочастинок.
Тунельний ефект: проходження мiкрочастинок через
потенцiйний бар'єр
 |
Нехай мiкрочастинка рухається уздовж осi
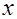 у просторi, в якому силове поле змiнюється стрибком (рис. 4). У областi 1, що простягається вiд
у просторi, в якому силове поле змiнюється стрибком (рис. 4). У областi 1, що простягається вiд 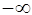 до 0,
до 0, 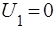 ; У областi 2, що простягається вiд 0 до
; У областi 2, що простягається вiд 0 до 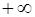 , потенцiйна енергiя дорiвнює
, потенцiйна енергiя дорiвнює 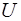 . Перехід з областi 1 у область 2 створює потенцiйний бар'єр висотою
. Перехід з областi 1 у область 2 створює потенцiйний бар'єр висотою 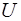 .
.
Рис. 4. Нескiнченно протягнутий прямокутний
потенцiйний бар'єр висотою 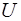 .
.
Рух мiкрочастинки описується рiвнянням Шредiнгера (11). Напишемо його для областей 1 та 2.
Для областi 1:
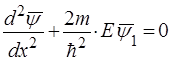 або
або  ,
,  (40)
(40)
де 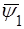 - хвильова функцiя мiкрочастинки у областi 1, та
- хвильова функцiя мiкрочастинки у областi 1, та
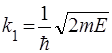 . (41)
. (41)
Для областi 2:
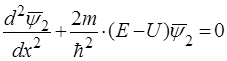 або
або 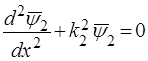 , (42)
, (42)
де 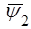 - хвильова функцiя мiкрочастинки у областi 2, та
- хвильова функцiя мiкрочастинки у областi 2, та
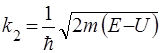 . (43)
. (43)
Загальне рiшення рiвнянь (40) та (42) має такий вигляд:
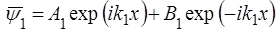 , де
, де 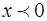 , (44)
, (44)
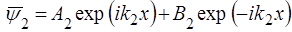 , де
, де 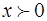 . (45)
. (45)
Доданок 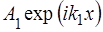 вiдповiдає хвилi, що розповсюджується у областi 1 у напрямку осi
вiдповiдає хвилi, що розповсюджується у областi 1 у напрямку осi 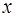 ,
, 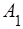 - амплiтуда цiєї хвилi. Доданок
- амплiтуда цiєї хвилi. Доданок  вiдповiдає хвилi, що розповсюджується у областi 1 у напрямку, протилежному
вiдповiдає хвилi, що розповсюджується у областi 1 у напрямку, протилежному 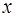 . Це хвиля, вiдбита вiд бар'єру,
. Це хвиля, вiдбита вiд бар'єру, 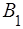 - амплiтуда вiдбитої хвилi. Імовiрнiсть знаходження мiкрочастинки у тому чи iншому мiсцi простору пропорцiйна квадрату амплiтуди хвилi де Бройля, тому вiдношення
- амплiтуда вiдбитої хвилi. Імовiрнiсть знаходження мiкрочастинки у тому чи iншому мiсцi простору пропорцiйна квадрату амплiтуди хвилi де Бройля, тому вiдношення
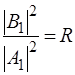 (46)
(46)
- коефiцiєнт вiдбиття мiкрочастинки вiд бар'єру.
Доданок 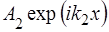 відповідає хвилі, що розповсюджується у областi 2 у напрямку осi
відповідає хвилі, що розповсюджується у областi 2 у напрямку осi 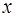 . Квадрат амплiтуди цiєї хвилi відображає iмовiрнiсть проникнення мiкрочастинки у область 2. Вiдношення
. Квадрат амплiтуди цiєї хвилi відображає iмовiрнiсть проникнення мiкрочастинки у область 2. Вiдношення
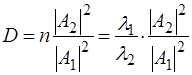 (47)
(47)
- коефiцiєнт прозоростi бар'єру, 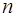 - показник заломлення хвилі де Бройля, що дорiвнює вiдношенню довжини хвиль
- показник заломлення хвилі де Бройля, що дорiвнює вiдношенню довжини хвиль
у областях 1 та 2: 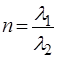 .
.
Доданок 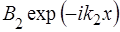 повинен відображати вiдбиту хвилю, що розповсюджується у областi 2. Такої хвилi немає, тому
повинен відображати вiдбиту хвилю, що розповсюджується у областi 2. Такої хвилi немає, тому 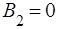 .
.
Iз закона збереження числа частинок виходить, що
 . (48)
. (48)
Можна показати, що для бар'єру, висота якого 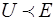 , коефiцiєнт вiдбиття
, коефiцiєнт вiдбиття
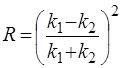 . (49)
. (49)
Такий бар'єр зветься низьким. У таблиці 1 наведено значення 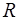 для рiзних значень
для рiзних значень 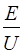 . Iз таблицi видно, що навiть у тому випадку, коли енергiя мiкрочастинки перевищує висоту бар'єру, коефiцiєнт вiдбиття не рiвний нулю: мiкрочастинка має деяку iмовiрнiсть вiдбитися вiд такого бар'єру. Класична частинка у цьому випадку без перешкоджень пройшла б з першої областi у другу, помiнявши лише свою енергiю. При
. Iз таблицi видно, що навiть у тому випадку, коли енергiя мiкрочастинки перевищує висоту бар'єру, коефiцiєнт вiдбиття не рiвний нулю: мiкрочастинка має деяку iмовiрнiсть вiдбитися вiд такого бар'єру. Класична частинка у цьому випадку без перешкоджень пройшла б з першої областi у другу, помiнявши лише свою енергiю. При 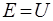 ,
, 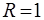 та проникнення мiкрочастинки у другу область неможливе; класична ж частинка з енергiєю
та проникнення мiкрочастинки у другу область неможливе; класична ж частинка з енергiєю 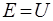 пройде у другу область, тiльки кiнетична енергiя її у цiй областi буде рiвна нулю.
пройде у другу область, тiльки кiнетична енергiя її у цiй областi буде рiвна нулю.
Таблиця 1
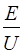
| 1,0 | 1,11 | 1,25 | 2,0 | |
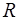
| 1,0 | 0,27 | 0,146 | 0,03 | 0,0007 |
У випадку високого бар'єру  хвильове число
хвильове число 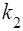 стає уявним. Припустимо, що:
стає уявним. Припустимо, що: 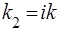 , де
, де 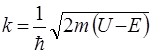 являється дiйсним числом. Тодi хвильовi функцiї y 1 та y 2 набудуть такого вигляду:
являється дiйсним числом. Тодi хвильовi функцiї y 1 та y 2 набудуть такого вигляду:
 ,
, 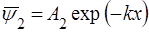 . (50)
. (50)
Оскiльки рiшення  не являється плоскою хвилею, воно не описує частинку всерединi бар'єру. Проте iз умови неперервностi хвильової функцiї очевидно, що для бар'єру кiнцевої товщини
не являється плоскою хвилею, воно не описує частинку всерединi бар'єру. Проте iз умови неперервностi хвильової функцiї очевидно, що для бар'єру кiнцевої товщини 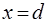 iмовiрнiсть знаходження частинки на зворотнiй стiнцi бар'єру дорiвнює:
iмовiрнiсть знаходження частинки на зворотнiй стiнцi бар'єру дорiвнює:
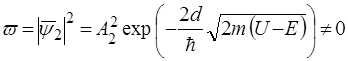 , (51)
, (51)
тобто, вiдмiнна вiд нуля. Цей факт показує можливiсть проходження (просочування) мiкрочастинок крiзь потенцiйний бар'єр кiнцевої товщини 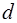 (рис. 5а). Таке просочування одержало назву тунельного ефекту. На основi (51) коефiцiєнт прозоростi такого бар'єру дорiвнює:
(рис. 5а). Таке просочування одержало назву тунельного ефекту. На основi (51) коефiцiєнт прозоростi такого бар'єру дорiвнює:
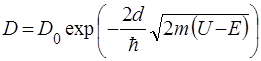 , (52)
, (52)
де 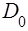 - коефiцiєнт пропорцiйностi, за порядком величини близькій до одиницi.
- коефiцiєнт пропорцiйностi, за порядком величини близькій до одиницi.


А б
Рис. 5. Потенцiйний бар'єр кiнцевої товщини:
а - прямокутний; б - довiльної форми.
У таблиці 2 приведена величина 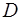 для бар'єрiв рiзної товщини, але однаковій висоти
для бар'єрiв рiзної товщини, але однаковій висоти 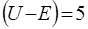 еВ. З даних таблиці 2 видно, що бар'єри помiж атомами у кристалах, що мають
еВ. З даних таблиці 2 видно, що бар'єри помiж атомами у кристалах, що мають 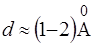 володiють достатньо високою прозорiстю.
володiють достатньо високою прозорiстю.
Таблиця 2
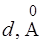
| 1,0 | 1,5 | 2,0 | 5,0 |
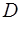
| 0,1 | 0,03 | 0,008 | 5,5.10-7 |
Для бар'єру довiльної форми (рис. 5б) узагальнення формулы (52) приводить до такого виразу коефiцiєнта прозоростi:
 , (53)
, (53)
де 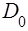 - величина, близька до одиницi.
- величина, близька до одиницi.
Чудовим являється те, що при тунельнiм просочуваннi крiзь потенцiальний бар'єр енергiя мiкрочастинок не змiнюється: вони покидають бар'єр з такою ж енергiєю, з якою входять до нього.
Тунельний ефект грає велику роль у електронiцi. Вiн може обумовлювати протiкання таких явищ, як емiсiя електронiв пiд дiєю сильного поля, проходження струму через тонкi дiелектричнi плiвки, пробiй р-n -переходу. На його основi створенi напiвпровiдниковi тунельнi дiоди, розроблюються активнi плiвковi елементи та т.i.
Рух мiкрочастинки у обмеженiй областi простору. Квантування енергiї
Роздивимося рух мiкрочастинки, наприклад, електрона, у потенцiйнiй ямi (рис. 6). Для електрона такою ямою являється, наприклад, шматок металу: поза металу потенцiйна енергiя вiльного електрону 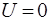 , усерединi металу
, усерединi металу 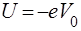 , де
, де 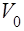 - позитивний потенцiал поля, створений вузлами гратки. Електрон не може вiльно покинути метал. Для виходу з нього електрону потрiбно зробити роботу, чисельно рiвну
- позитивний потенцiал поля, створений вузлами гратки. Електрон не може вiльно покинути метал. Для виходу з нього електрону потрiбно зробити роботу, чисельно рiвну 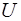 .
.
Для опису руху електрона у такiй ямi зручнiше вiсь х поєднати з дном ями та розбити простiр на три областi. Запишемо рiвняння Шедiнгера для цих областей.

Рис. 6. Електрон у прямокутній потенцiйній ямі
Області 1 і 3 ідентичні, тоді:

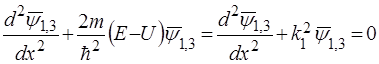 , (54)
, (54)
де 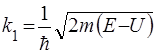 - уявна величина. (55)
- уявна величина. (55)
Загальним рiшенням рiвняння (54) буде:
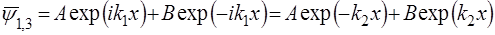 , (56)
, (56)
де  . (57)
. (57)
Спростимо задачу, думаючи, що висота бар'єру 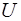 нескiнченно велика. Iз (57) виходить, що при
нескiнченно велика. Iз (57) виходить, що при 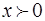 та
та 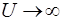 буде
буде 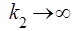 . Для того, щоб
. Для того, щоб 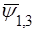 залишалася при цьому кiнцевою, необхiдно
залишалася при цьому кiнцевою, необхiдно 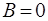 . З другого боку, щоб
. З другого боку, щоб 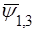 була кiнцевою та при
була кiнцевою та при 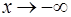 , необхiдно також
, необхiдно також 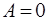 . Таким чином,
. Таким чином, 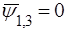 .
.
Область 2:
 , (58)
, (58)
де 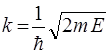 . (59)
. (59)
Загальним рiшенням рiвняння (58) буде:
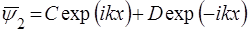 . (60)
. (60)
Скориставшись умовою неперервностi хвильової функцiї для лiвої стiнки потенцiйної ями, де 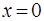 , запишемо:
, запишемо:
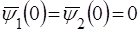 . (61)
. (61)
Тоді із (60) одержимо: 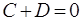 або
або 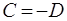 .
.
Пiдставимо це у (60) і знаходимо:
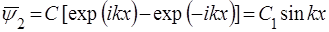 , (62)
, (62)
де 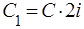 - наслiдок формули Ейлера з теорiї рядiв.
- наслiдок формули Ейлера з теорiї рядiв.
Для правої стiнки потенцiйної ями, де 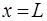 , з умови неперевностi запишемо:
, з умови неперевностi запишемо:
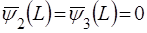 . (63)
. (63)
Тоді з (62) одержимо:
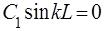 . (64)
. (64)
При 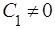 це можливо лише при
це можливо лише при 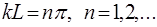
Звiдси знаходимо можливi значення 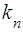 :
:
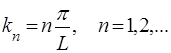 (65)
(65)
Пiдставляючи 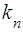 у (62), одержимо наступний вираз для хвильової функцiї
у (62), одержимо наступний вираз для хвильової функцiї 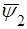 , яку позначимо через
, яку позначимо через 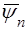 :
:
 . (66)
. (66)
Постiйна 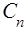 знаходиться iз умови нормування цiєї функцiї.
знаходиться iз умови нормування цiєї функцiї.
Енергiю стану, яка описується хвильовою функцiєю (66), одержимо, якщо пiдставимо 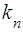 дисперсійну формулу у (34):
дисперсійну формулу у (34):
 . (67)
. (67)
 2015-08-21
2015-08-21 520
520








